LunchBox’s Form components enable users to create mathematically defined shapes.
Component Descriptions
Below, each component is described and visual examples are given. We’ve also included special Notes and Tips that can help users with less familiar situations.
Description
Appearance
3D Supershapes
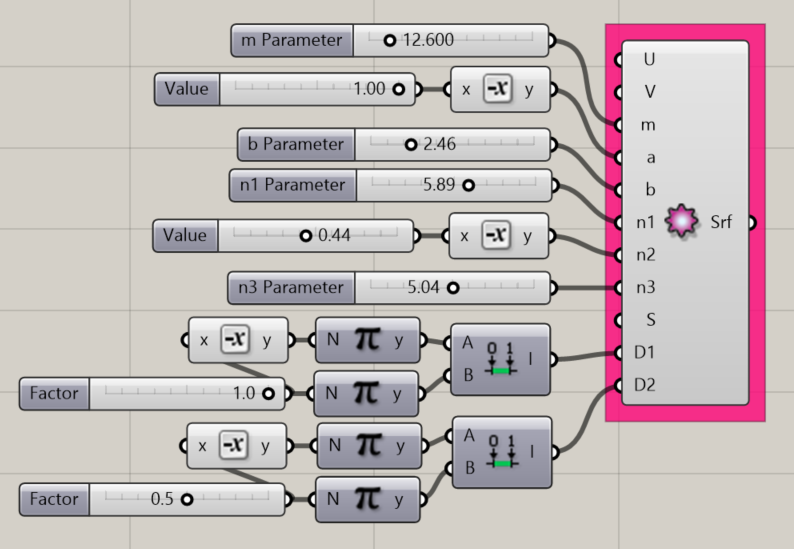
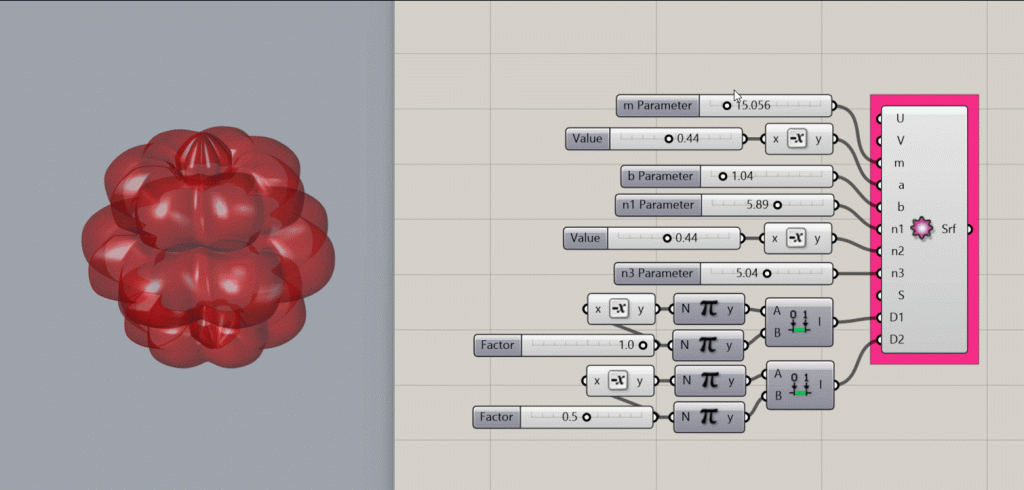
Creates a mathematical supershape at the origin of the Rhino document.
Learn more about supershapes here.
Input:
- A U Value. Tip: use an even number to close the shape
- A V Value
- An integer for the m parameter, which determines the frequency of the deformations.
- A b parameter
- An n1 parameter
- An n2 parameter
- An n3 parameter
- An S parameter, to set the scale of the object
- A domain for D1, which sets the number number of intervals in the horizontal direction. Tip: Set from -Pi to Pi to enclose the shape.
- A domain for D2, which sets the number of intervals in the vertical direction. Tip: Set from -Pi/2 to Pi/2 to enclose the shape.
Results:
- A supershape
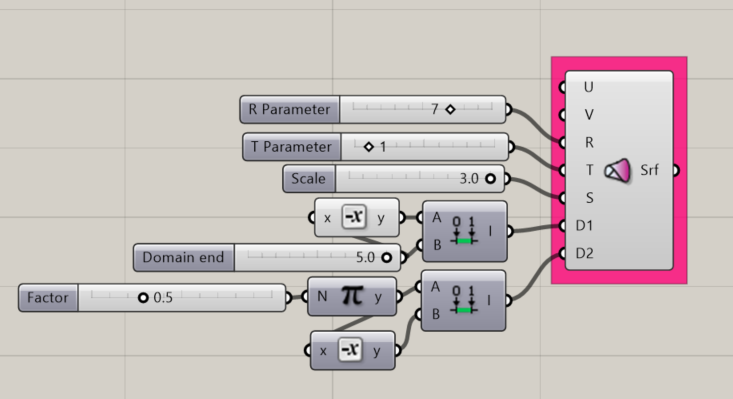
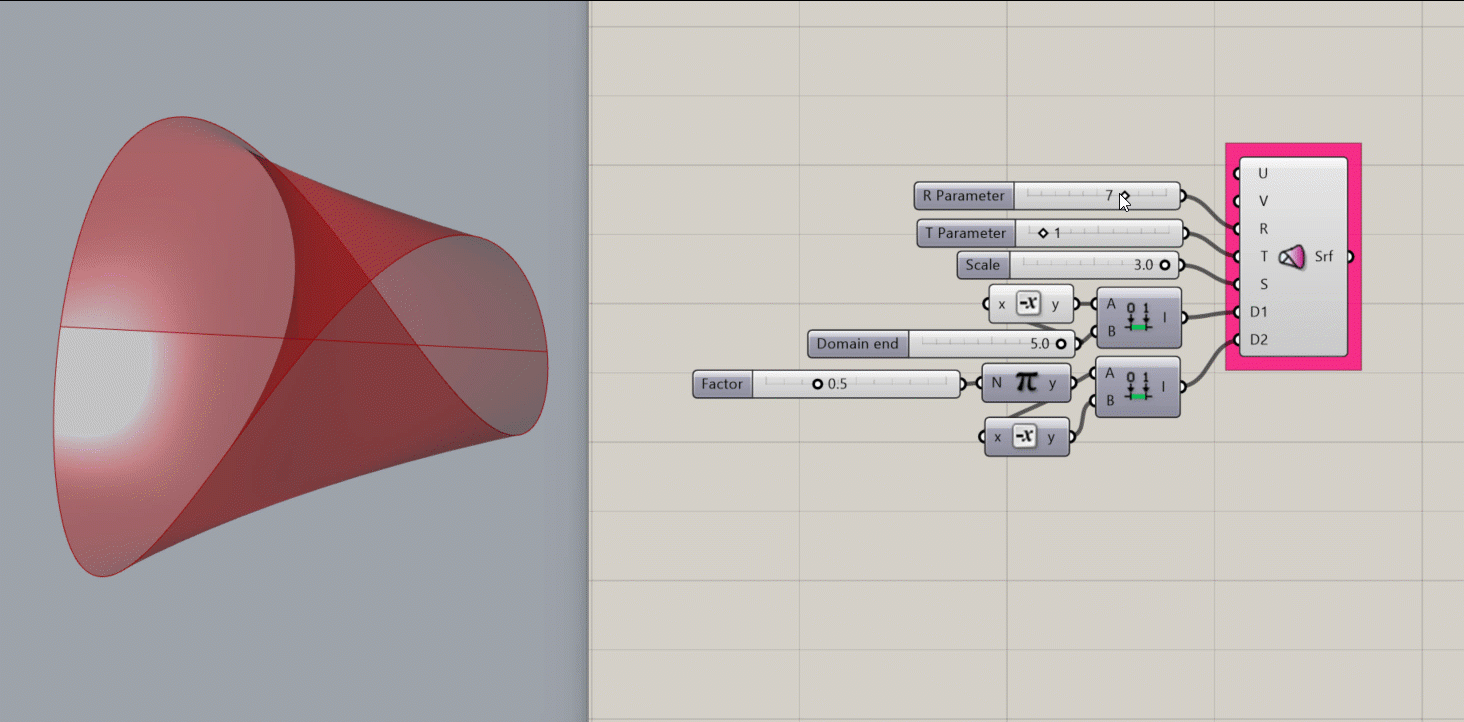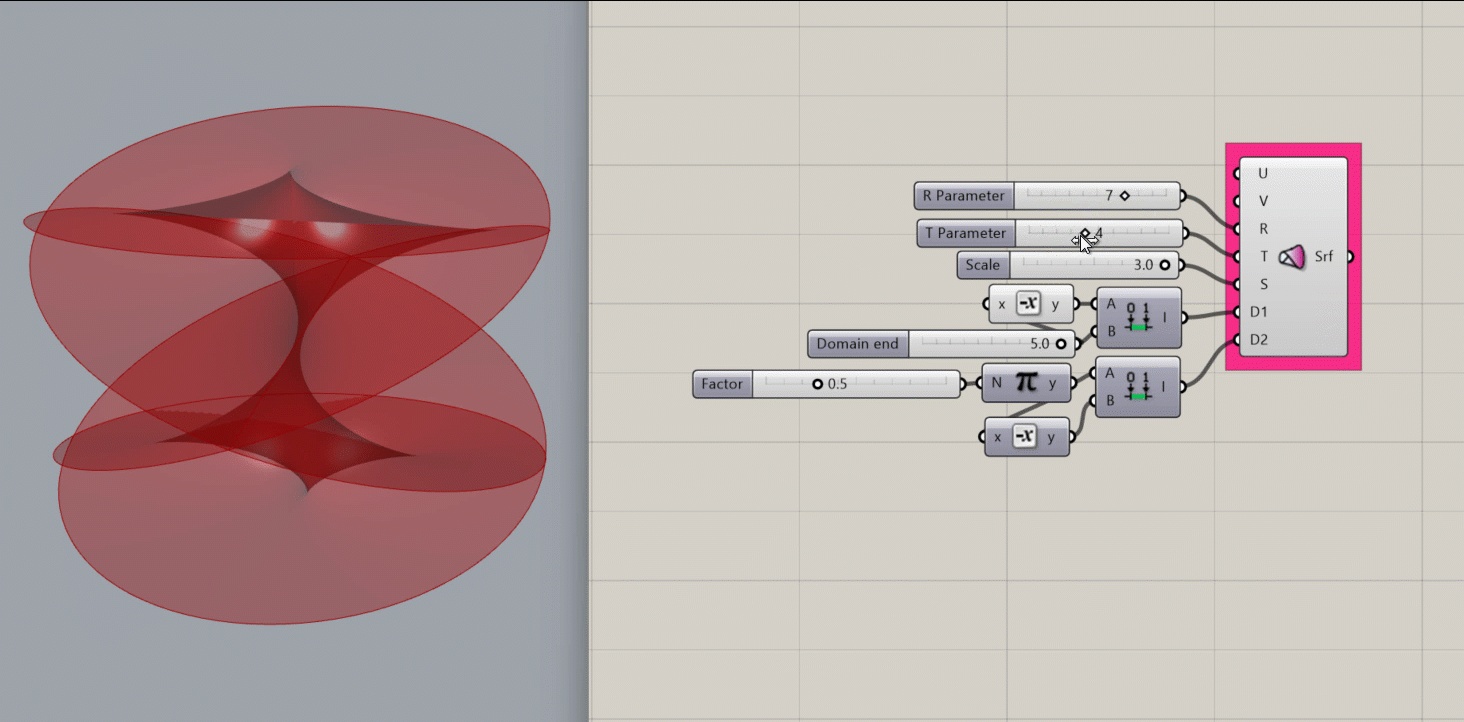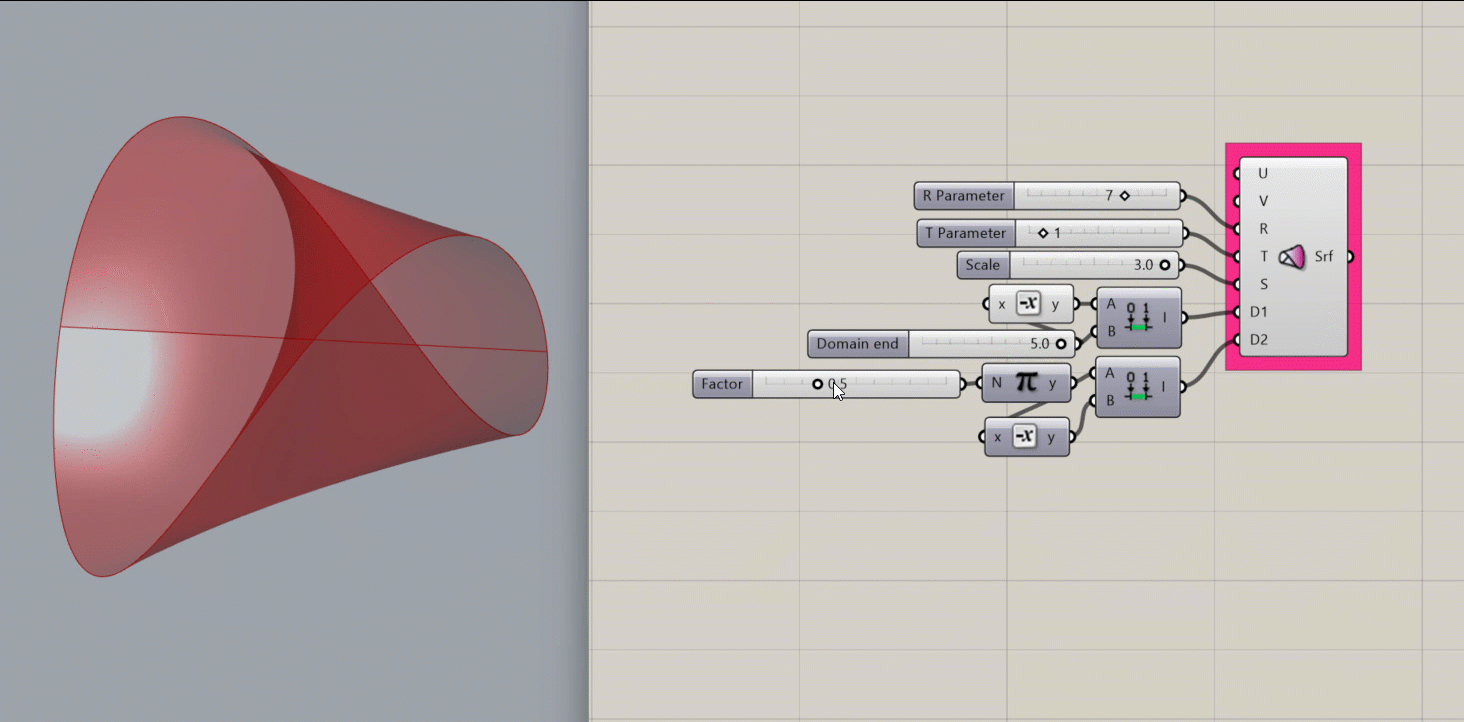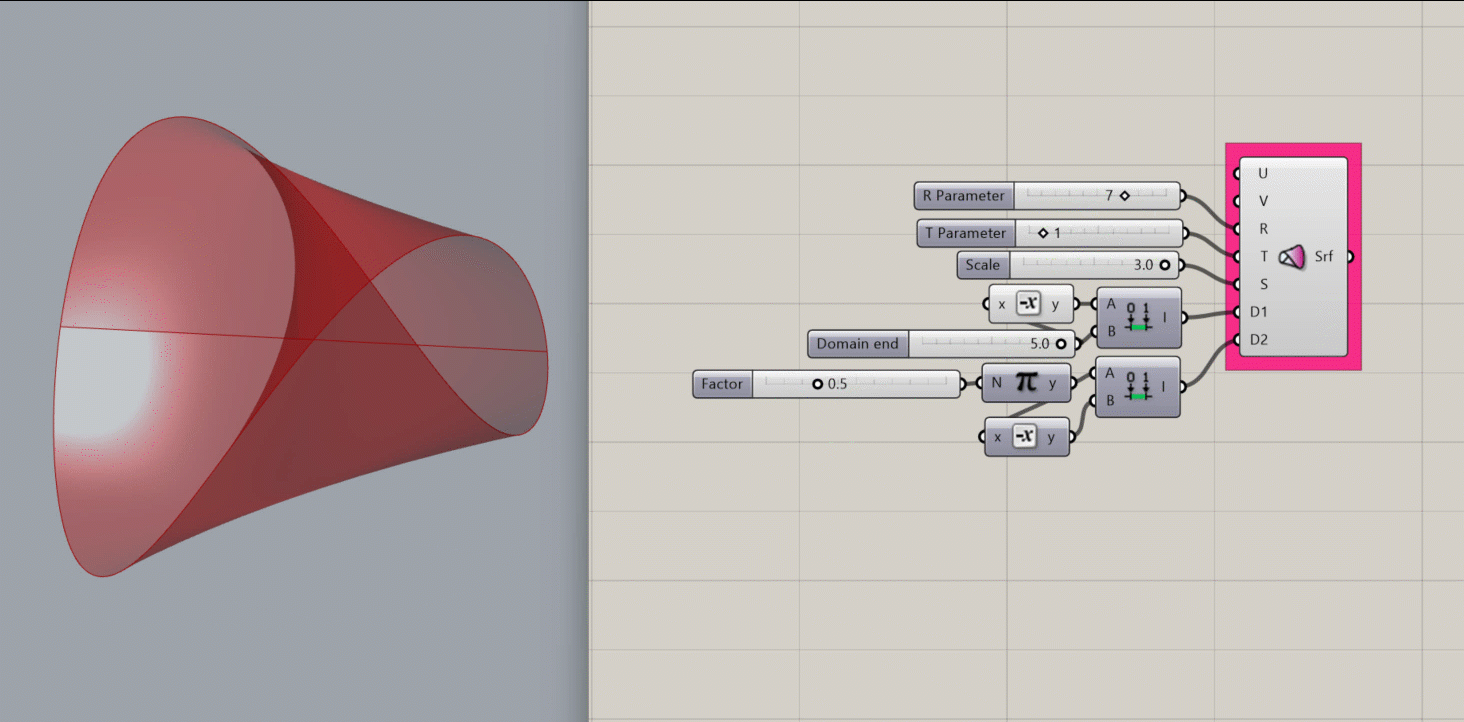
Conoid Surface
Creates a mathematical conoid surface.
Input:
- A U Value
- A V Value
- an R parameter, which affects the height of the shape
- A T parameter, which affects the number of revolutions of the shape.
- An S value, which scales the shape
- A domain for D1
- A domain for D2
Results:
- A conoid surface
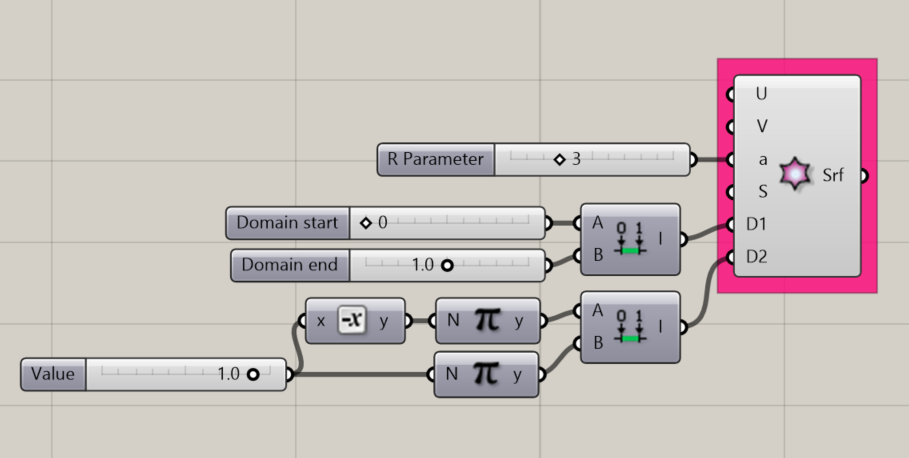
Enneper Surface
Creates a mathematical Enneper Surface, a self-intersecting minimal surface, at the origin of the Rhino document.
Input:
- A U Value
- A V Value
- an R parameter. This affects the frequency of the variations around the edges of the shape.
- A domain for D1, which affects the overall width of the shape.
- A domain for D2, which affects the radial area of the shape.
Results:
- An Enneper surface
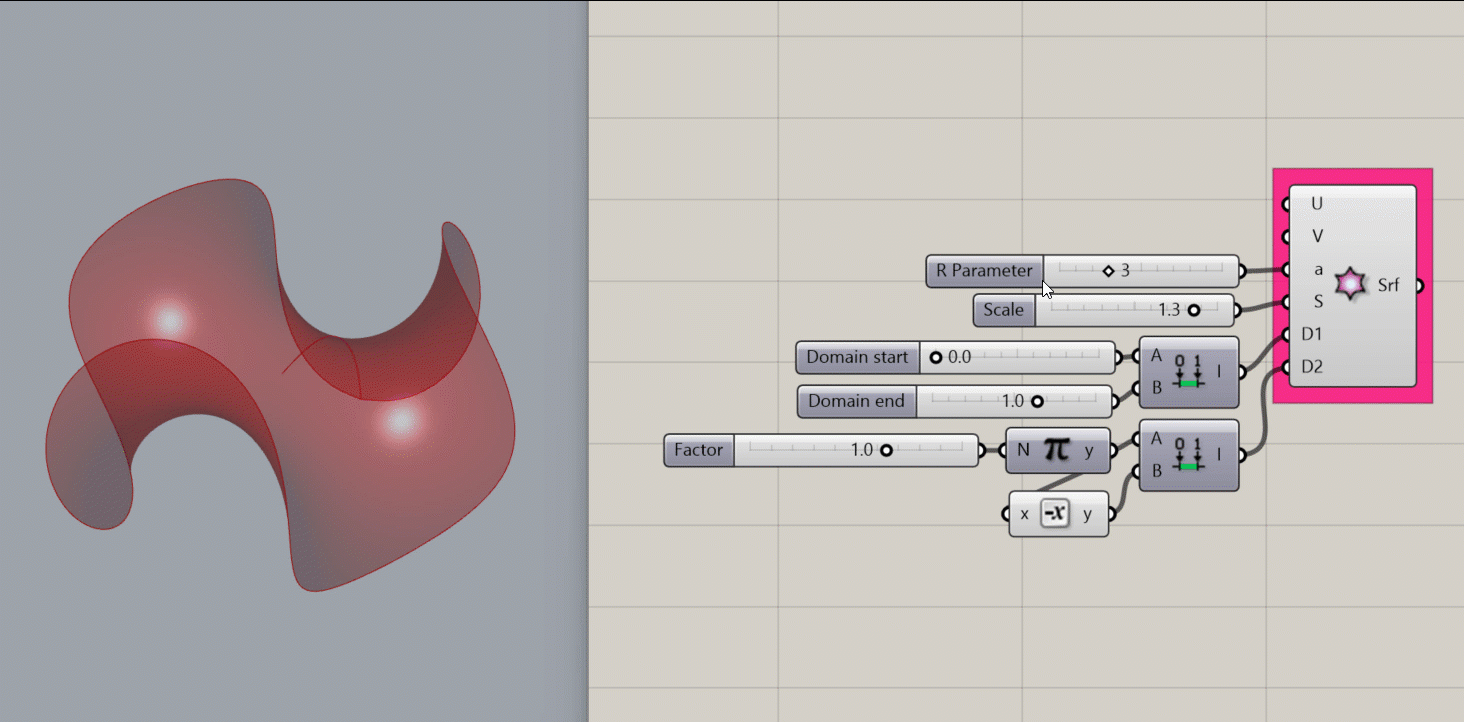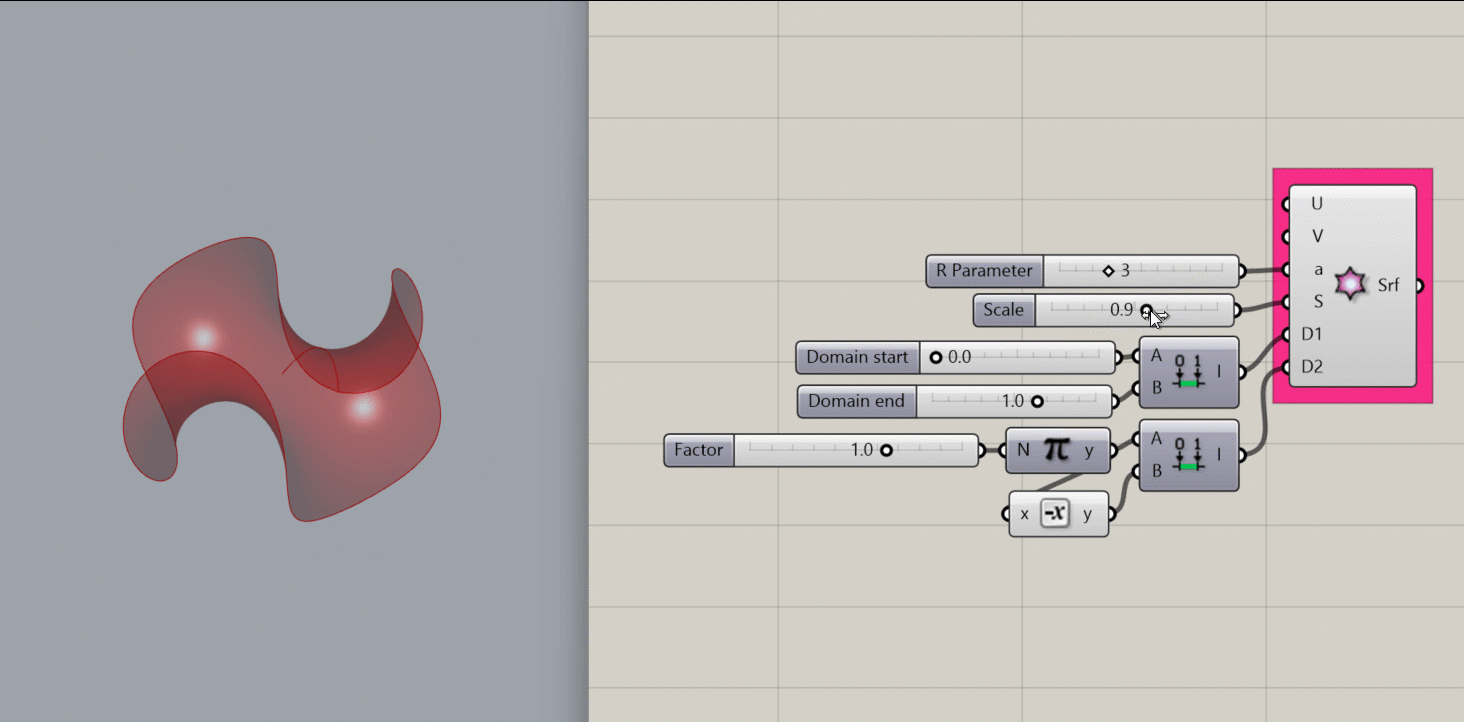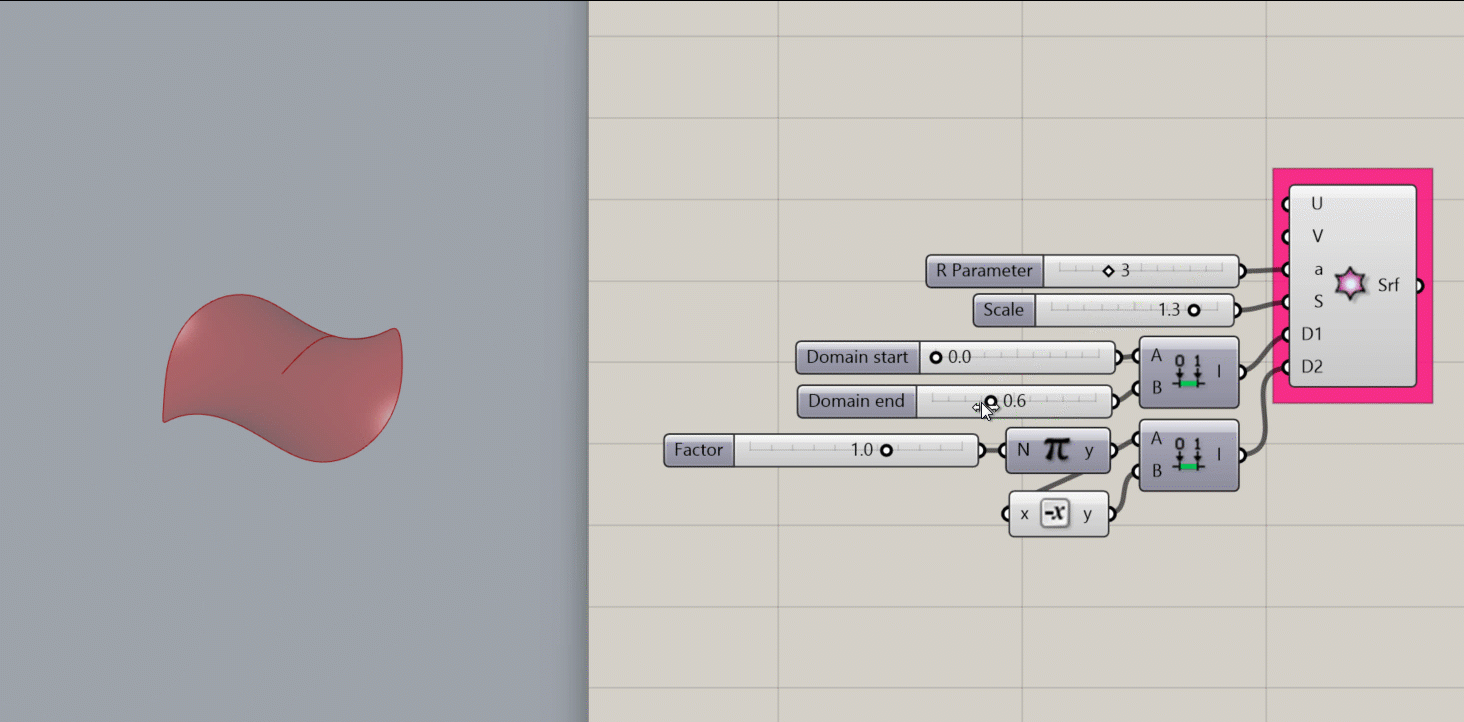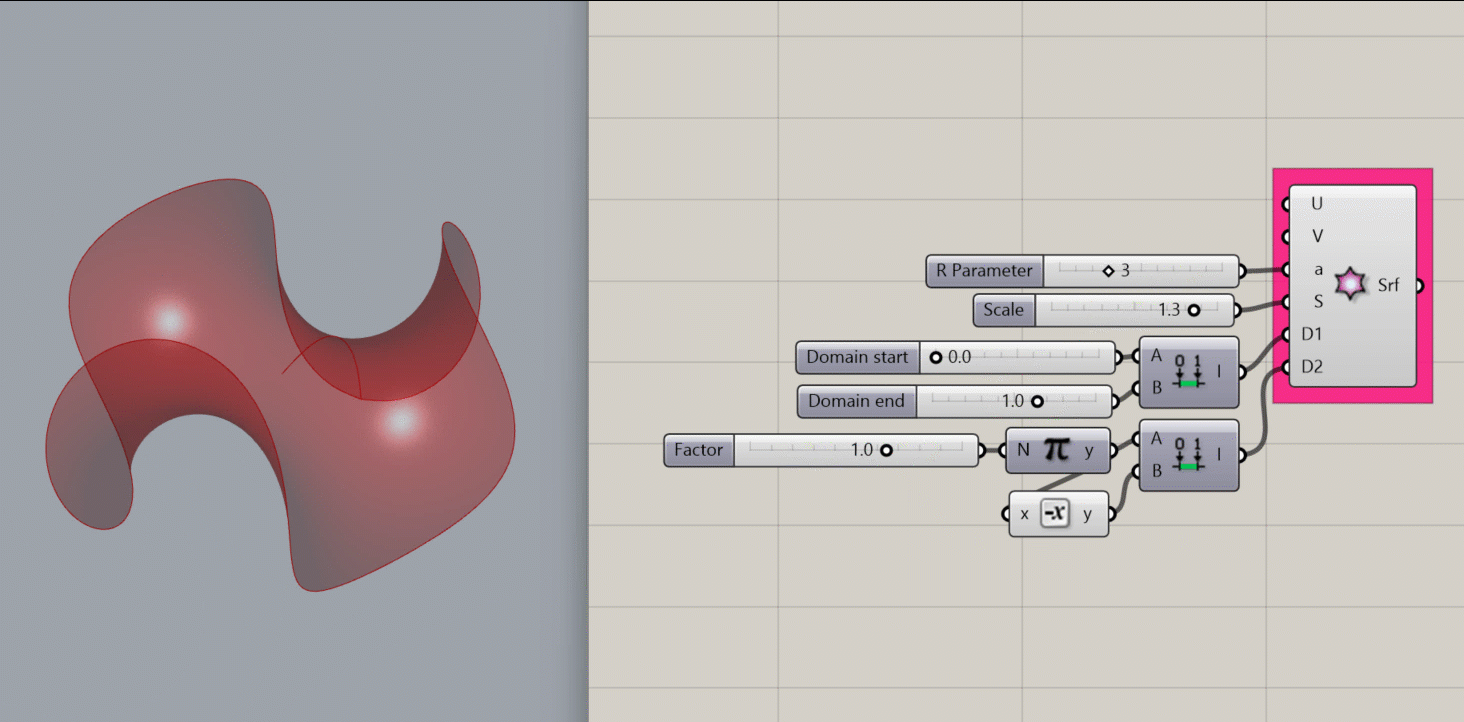
Helicoid Surface
Creates a Helicoid surface around the Rhino document’s origin point
Input:
- A U value
- A V value
- An integer for the R parameter, which affects the frequency width of the spiral in the V direction
- An integer for the T parameter, which subdivides the frequency width set by R
- An integer for S, which sets the scale of the object
- A domain for D1, which affects the outer radius of the object
- A domain for D2, which affects the height of the object (the number of periods)
Results:
- A helicoid surface
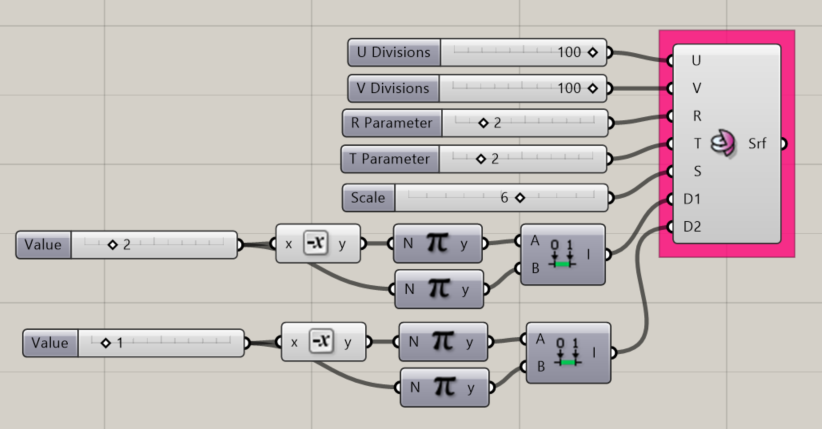
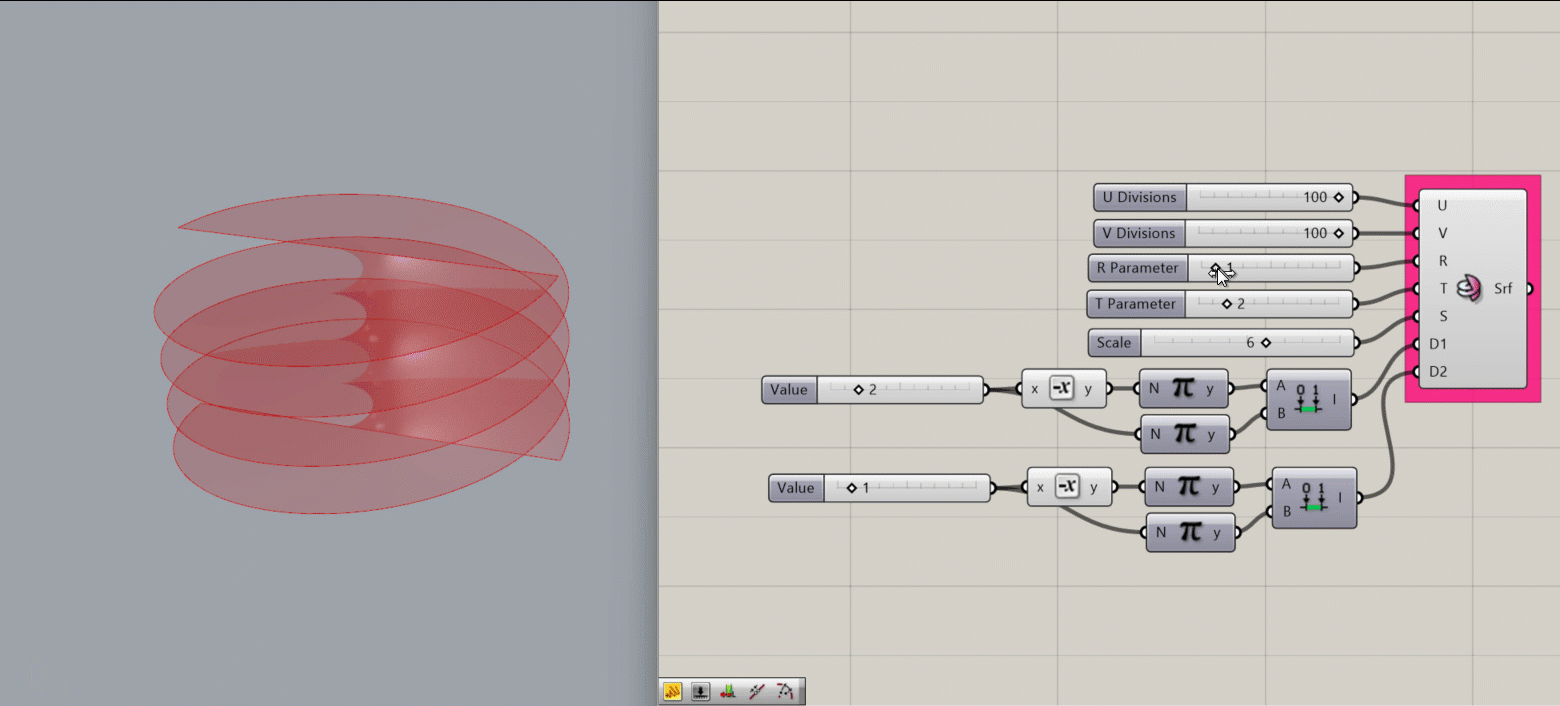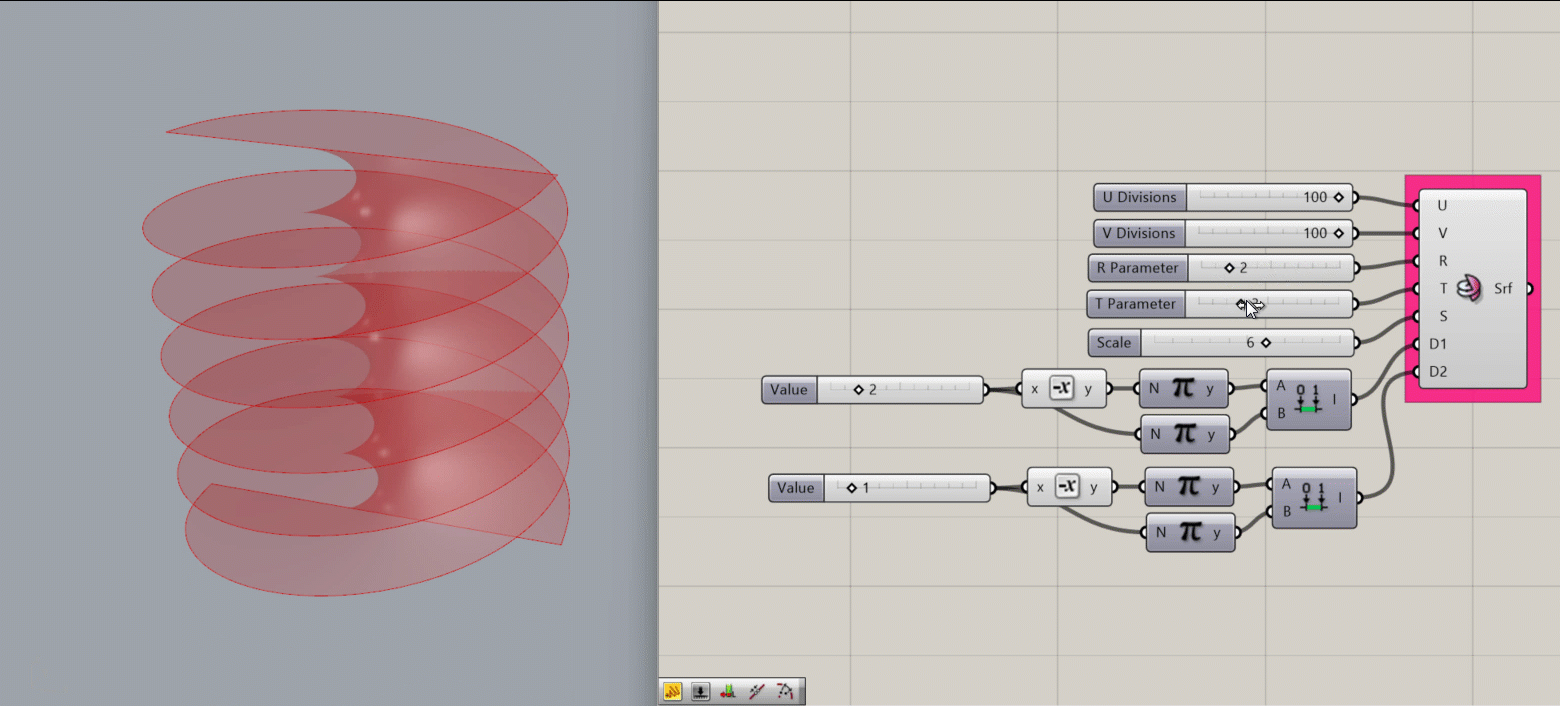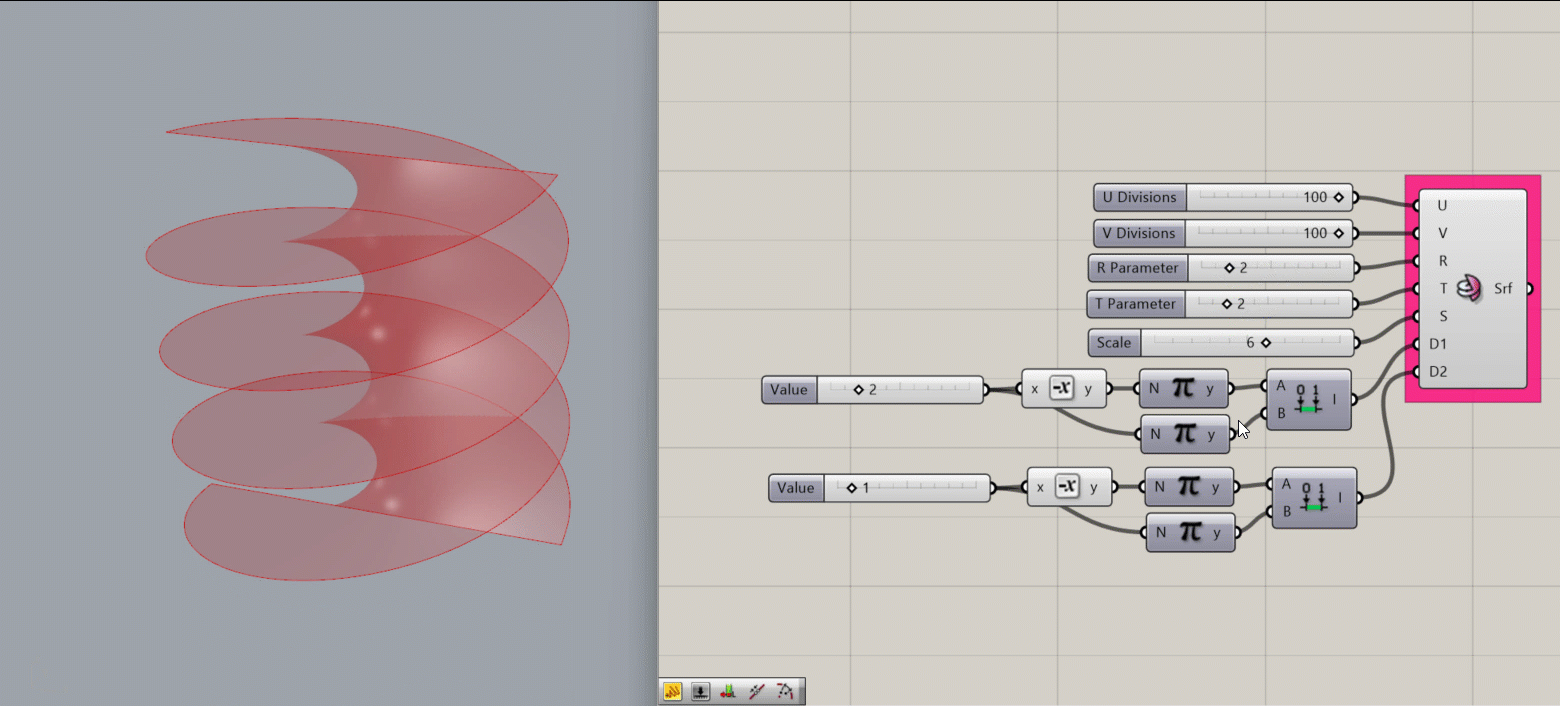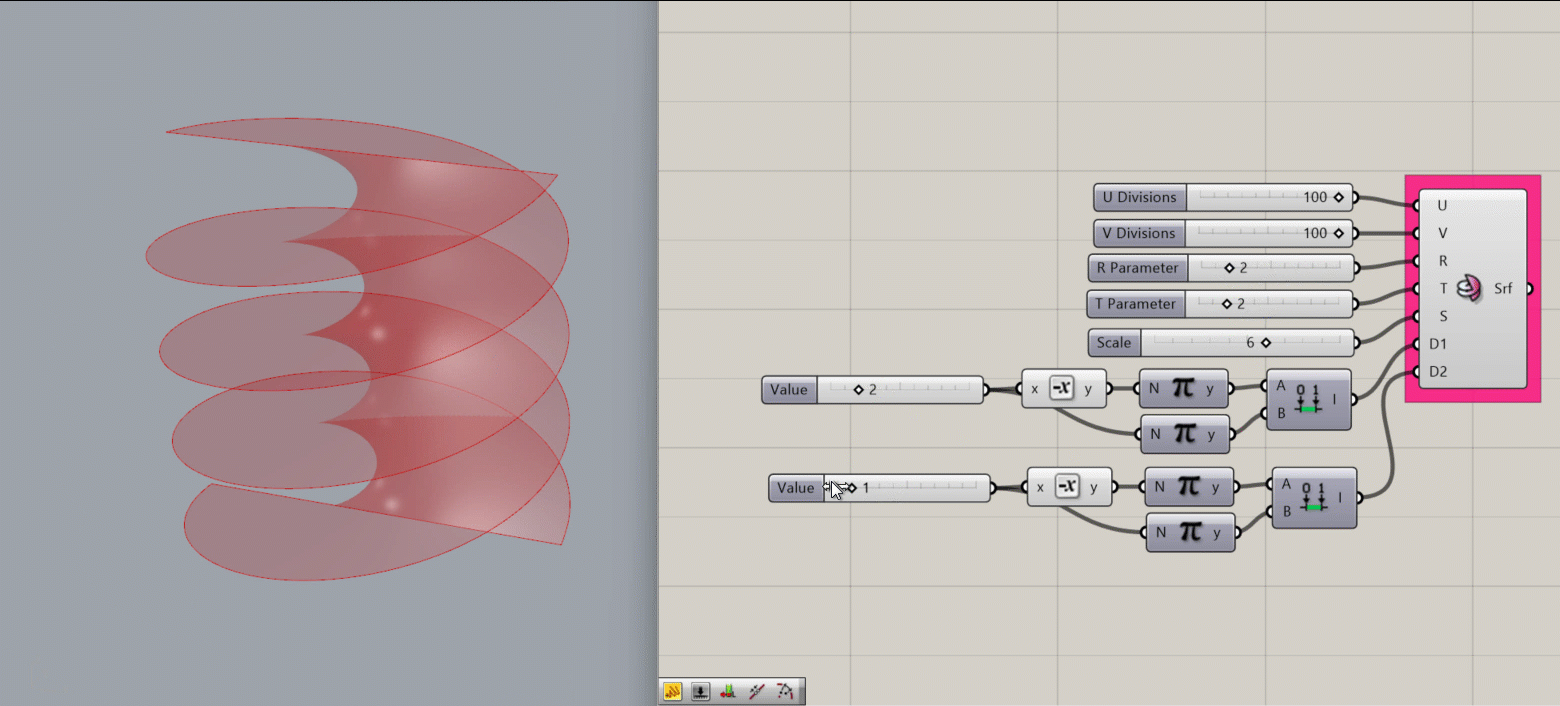
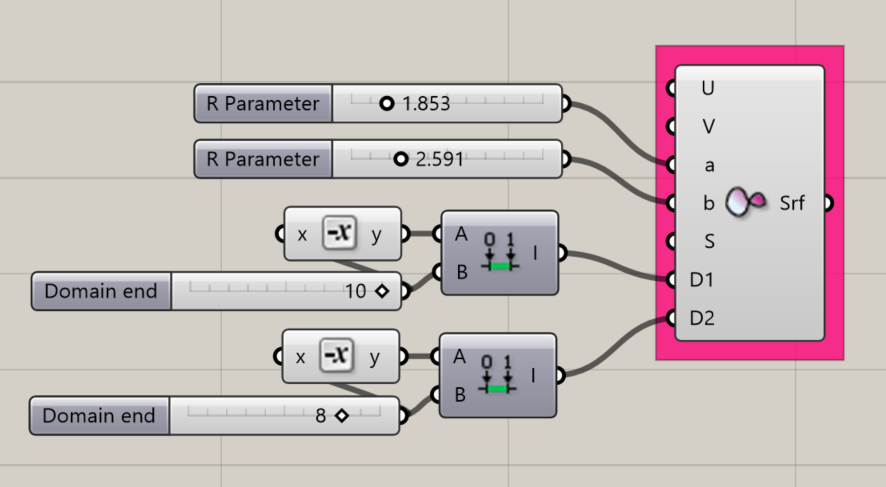
Hyperbolic Paraboloid
Creates a Hyperbolic Paraboloid
Input:
- A U value
- A V value
- A parameter for a, which sets the parabola width for the paraboloid in one direction
- A parameter for b, which sets the parabola width for the paraboloid in one direction
- An integer to set S, which affects the scale of the object
- A domain for D1, which affects the length of the Paraboloid
- A domain for D2, which affects the depth of the paraboloid
Results:
- A hyperbolic paraboloid shape
Klein Surface
Creates a mathematical Klein surface about the origin of the document.
Input:
- A U value
- A V value
- An integer for the R parameter, which affects width (radius) of the object
- An integer for the T parameter, which affects the incremental rotation of the cross sectional geometry of the object.
- An integer to set S, which affects the scale of the object
- A domain for D1, which affects length of the object. Note: 0 to 4Pi is 2 complete rotations.
- A domain for D2, which affects completion of the cross sectional geometry of the object. Note: 0 to Pi completes the rotation.
Results:
- A Klein surface
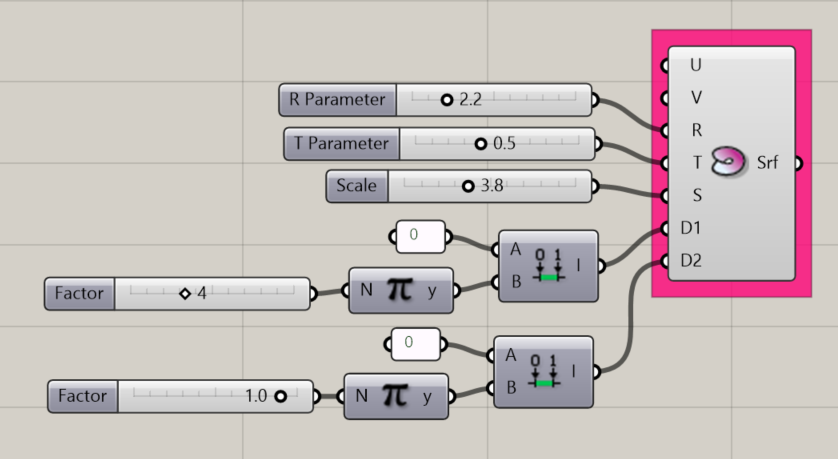
Mobius Surface
Creates a mathematical Mobius surface about the origin point of the document.
Input:
- A U value
- A V value
- An integer for the R parameter, which affects width (radius) of the object
- An integer for the T parameter, which affects the incremental rotation of the cross sectional geometry of the object.
- An integer to set S, which affects the scale of the object
- A domain for D1, which affects length of the object. Note: -Pi to Pi is 1 complete rotation.
- A domain for D2, which affects the width of the cross sectional geometry of the object, about the midpoint of the cross-section.
Results:
- A mobius surface
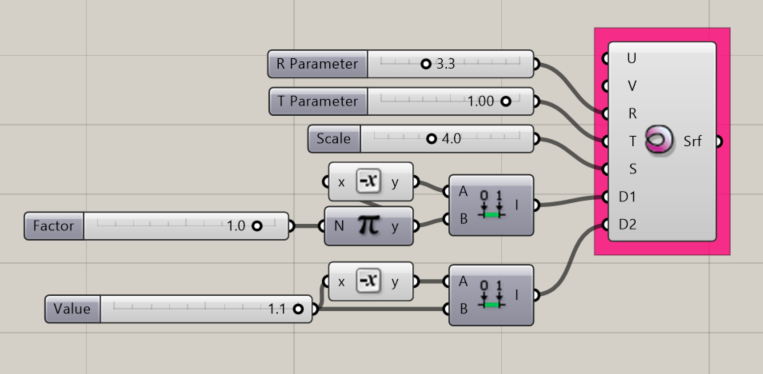
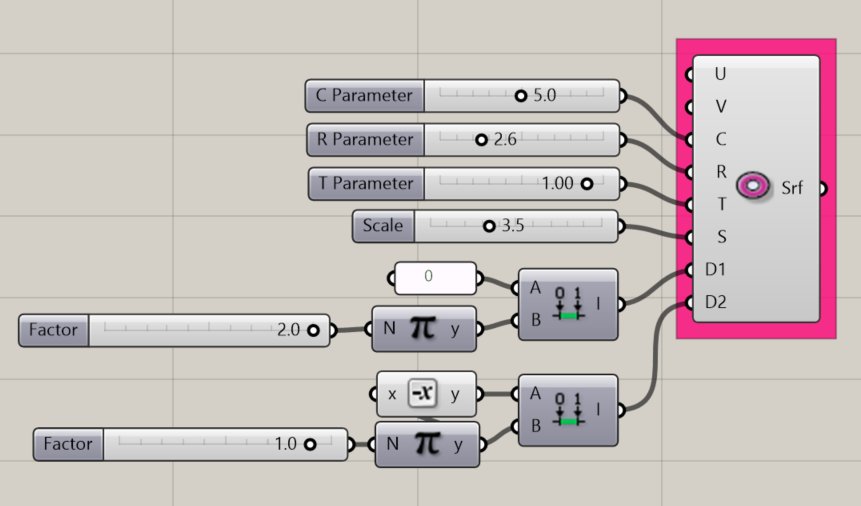
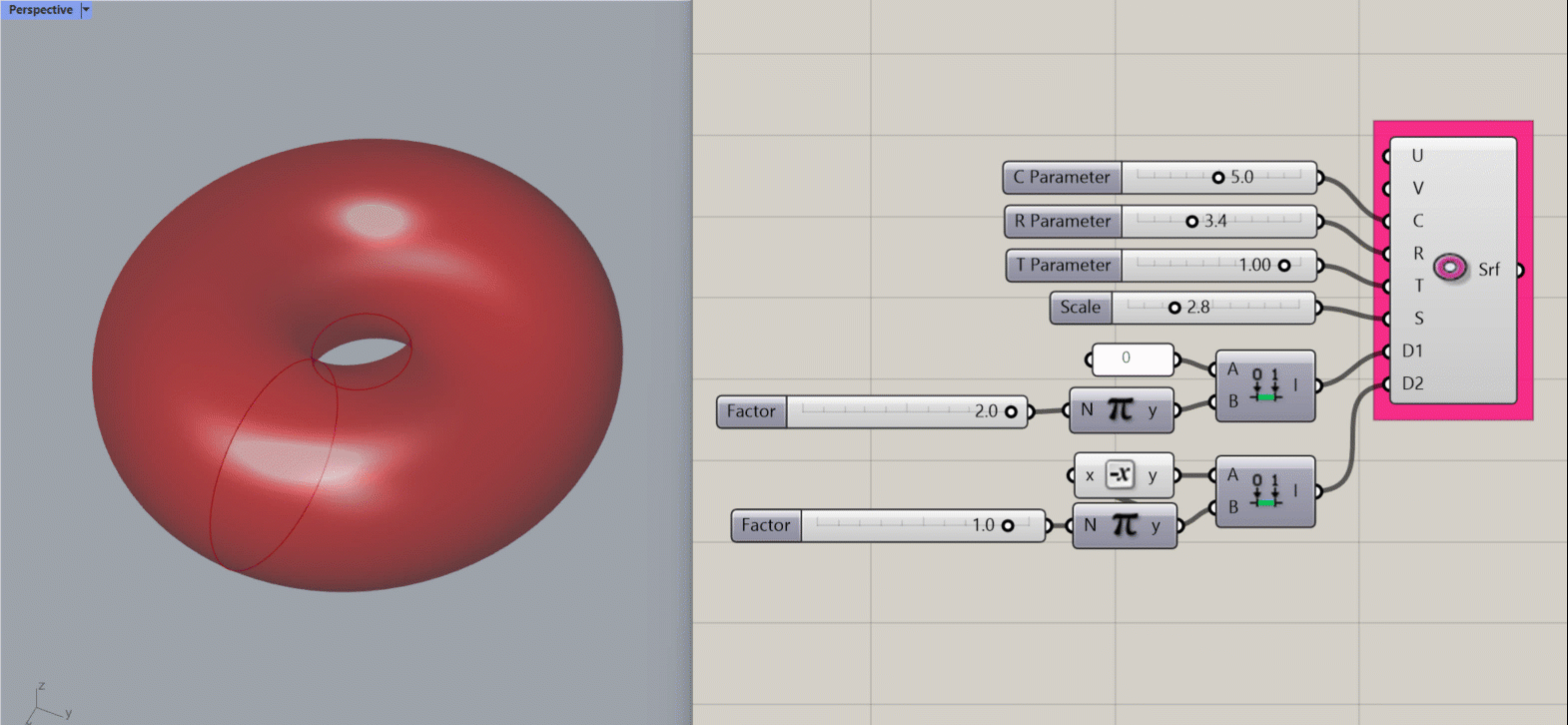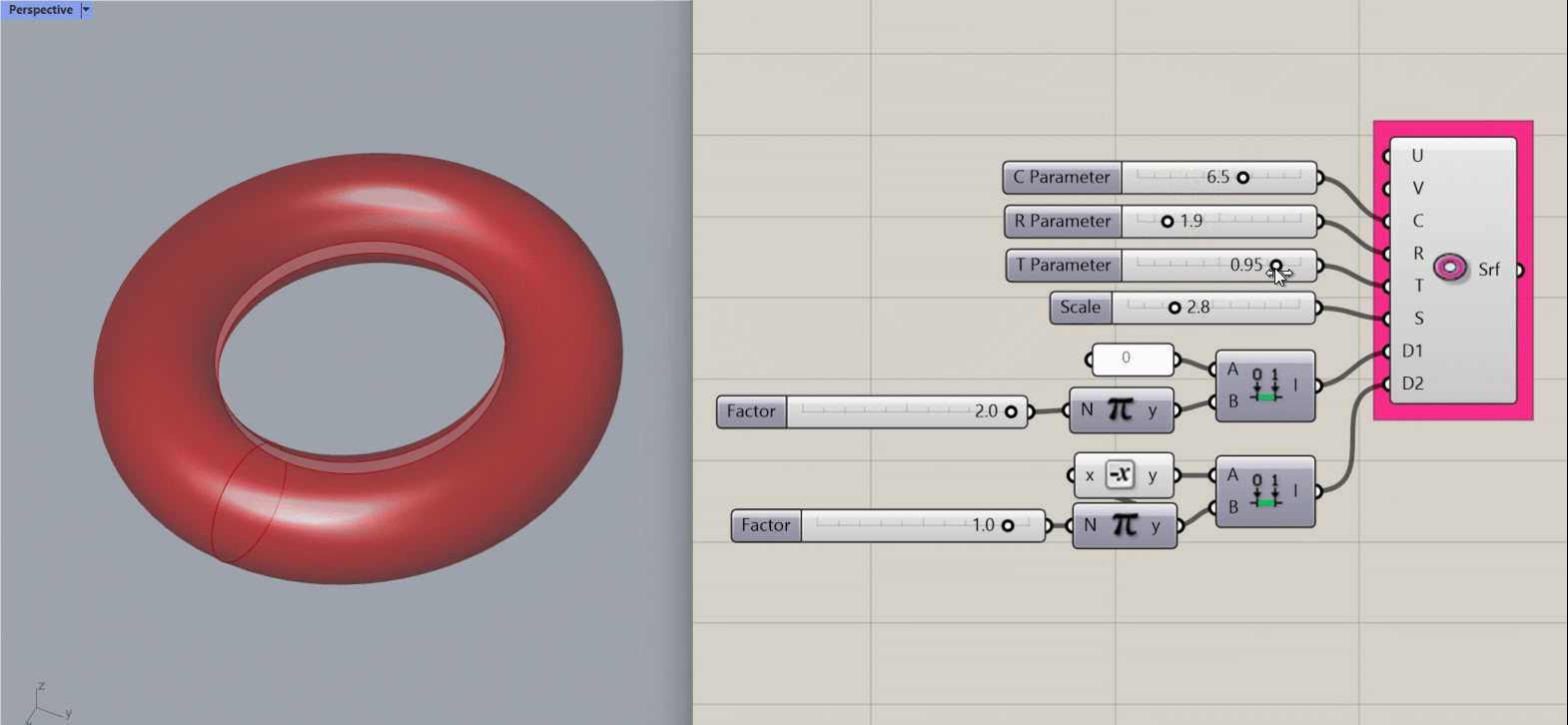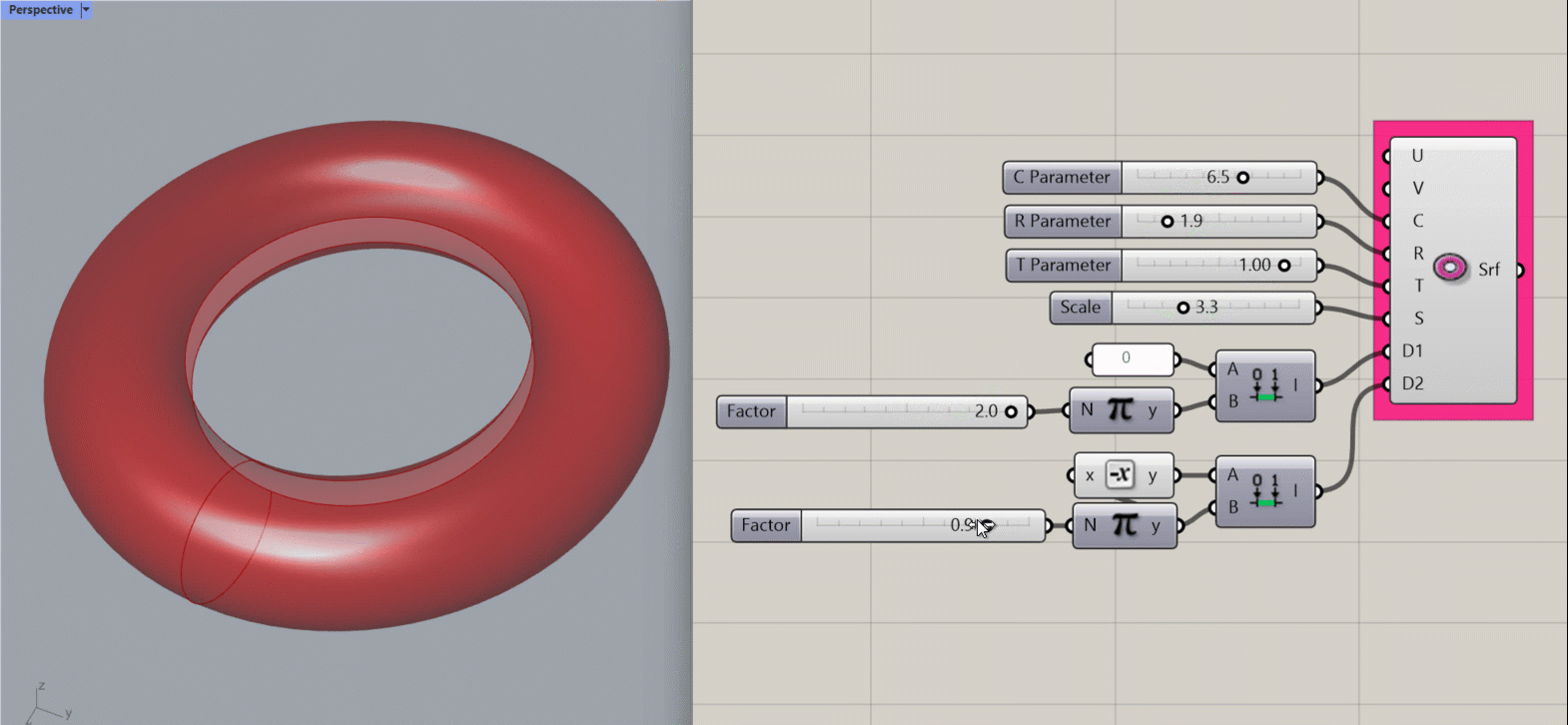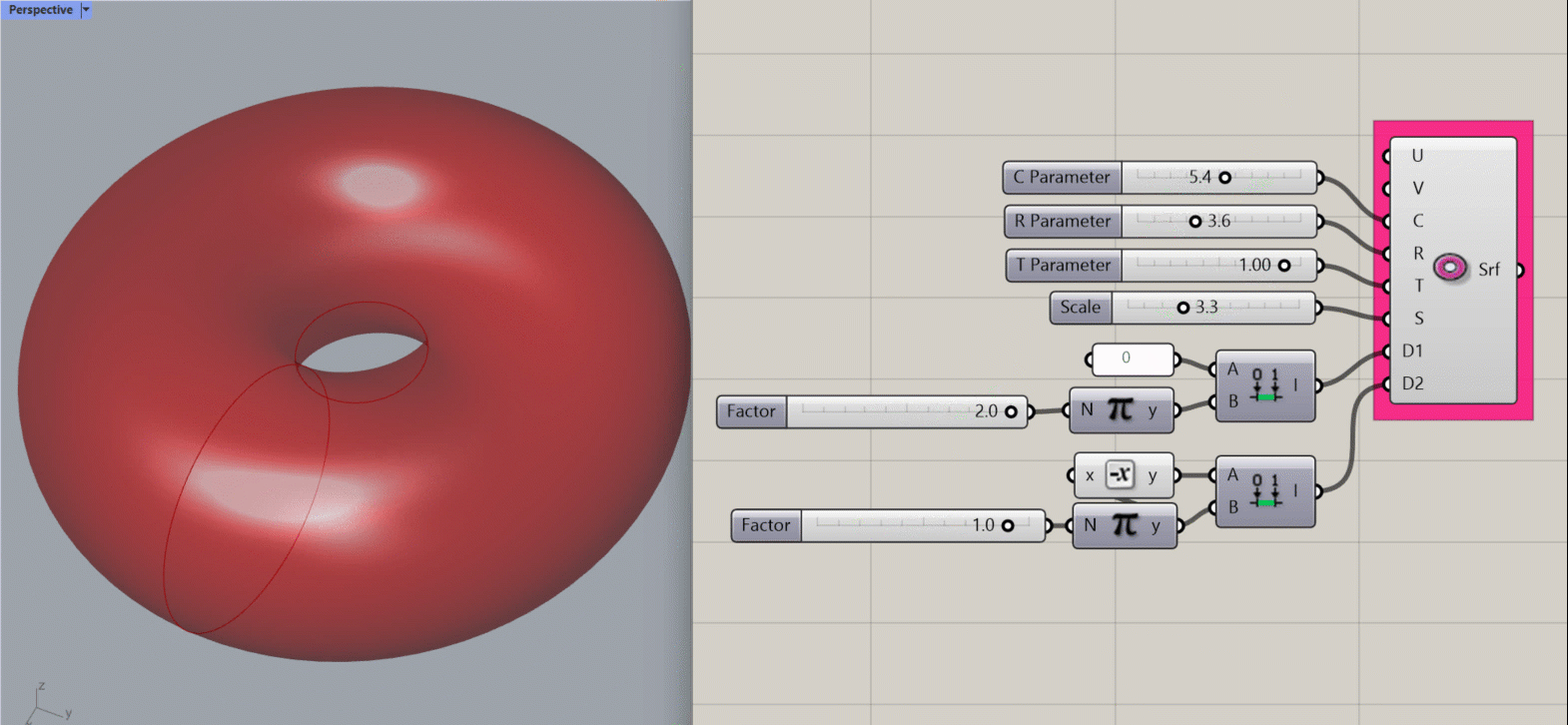
Torus Surface
Creates a mathematical torus (the most delicious of the mathematical surface shapes) about the origin point of the document.
Input:
- A U value
- A V value
- An integer for the C parameter, which affects width (radius) of the object
- An integer for the R parameter, which affects width (radius) of the cross-sectional geometry of the object
- An integer for the T parameter, which affects the length of the cross-sectional geometry of the object.
- An integer to set S, which affects the scale of the object
- A domain for D1, which affects the length of the object along its horizontal plane.
- A domain for D2, which affects the length of the object along its cross-sectional plane.
Results:
- A torus.
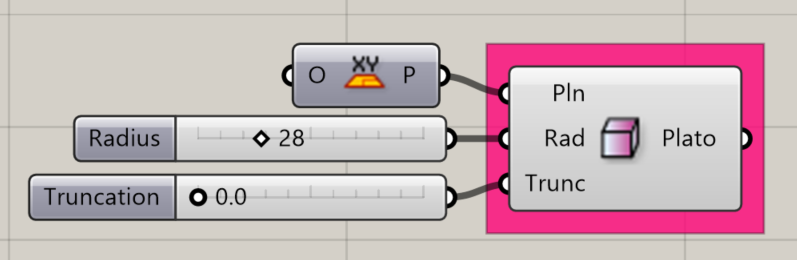
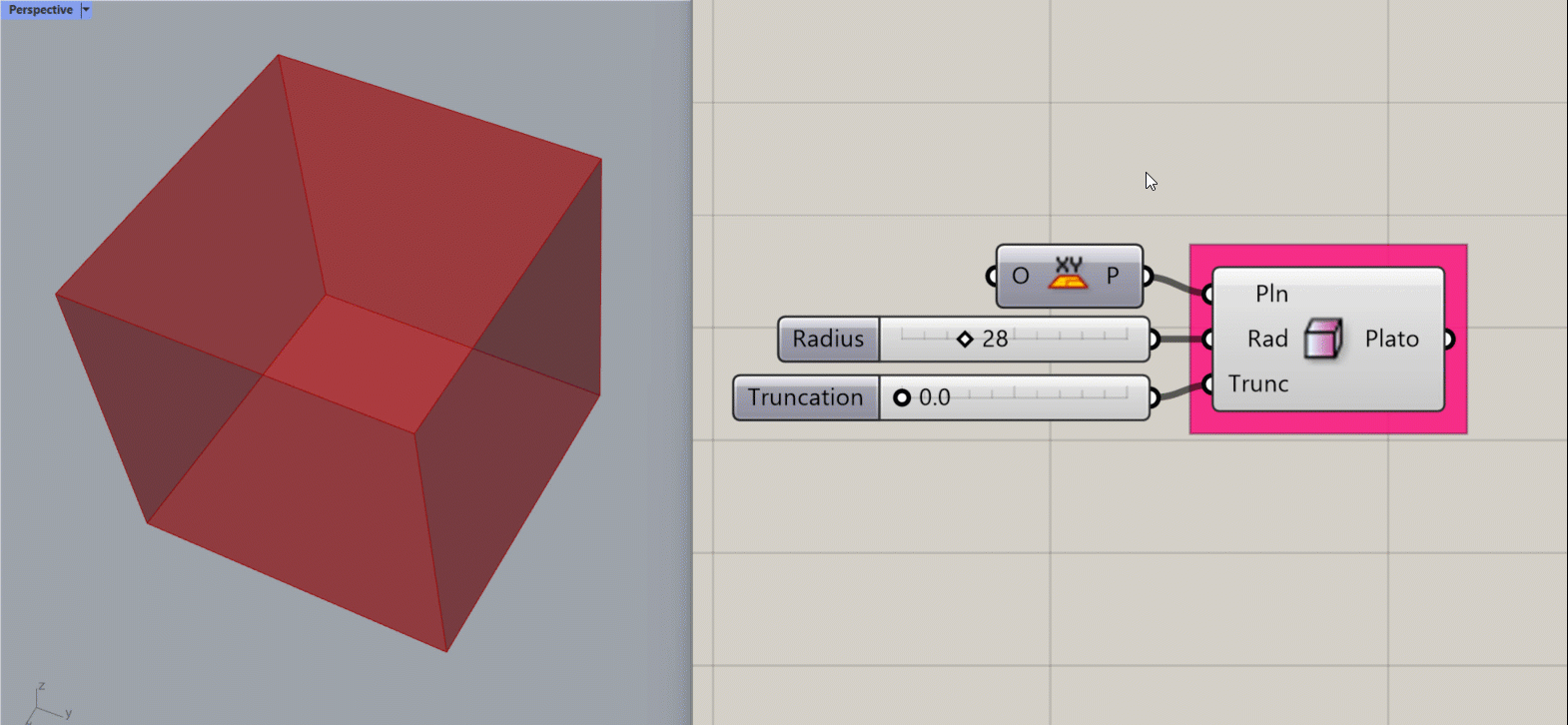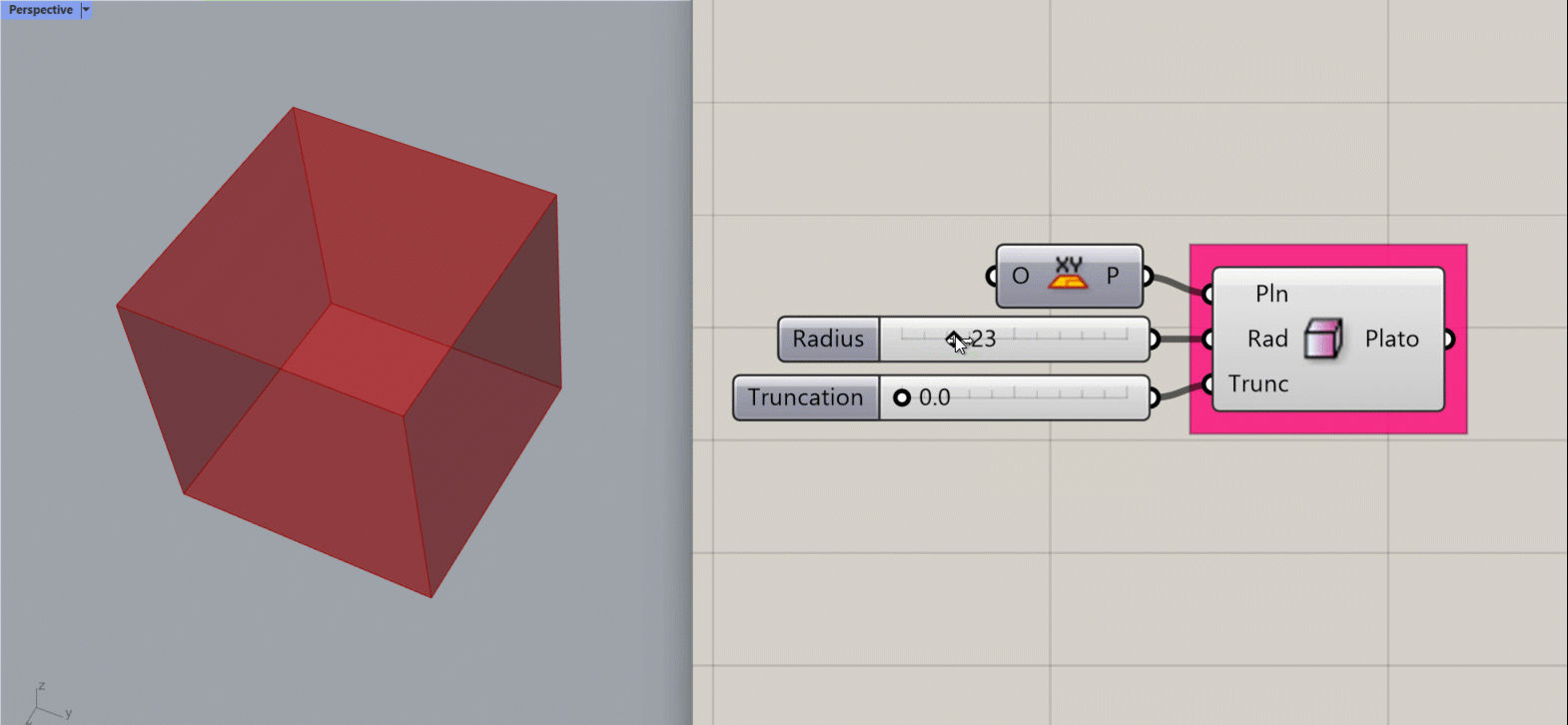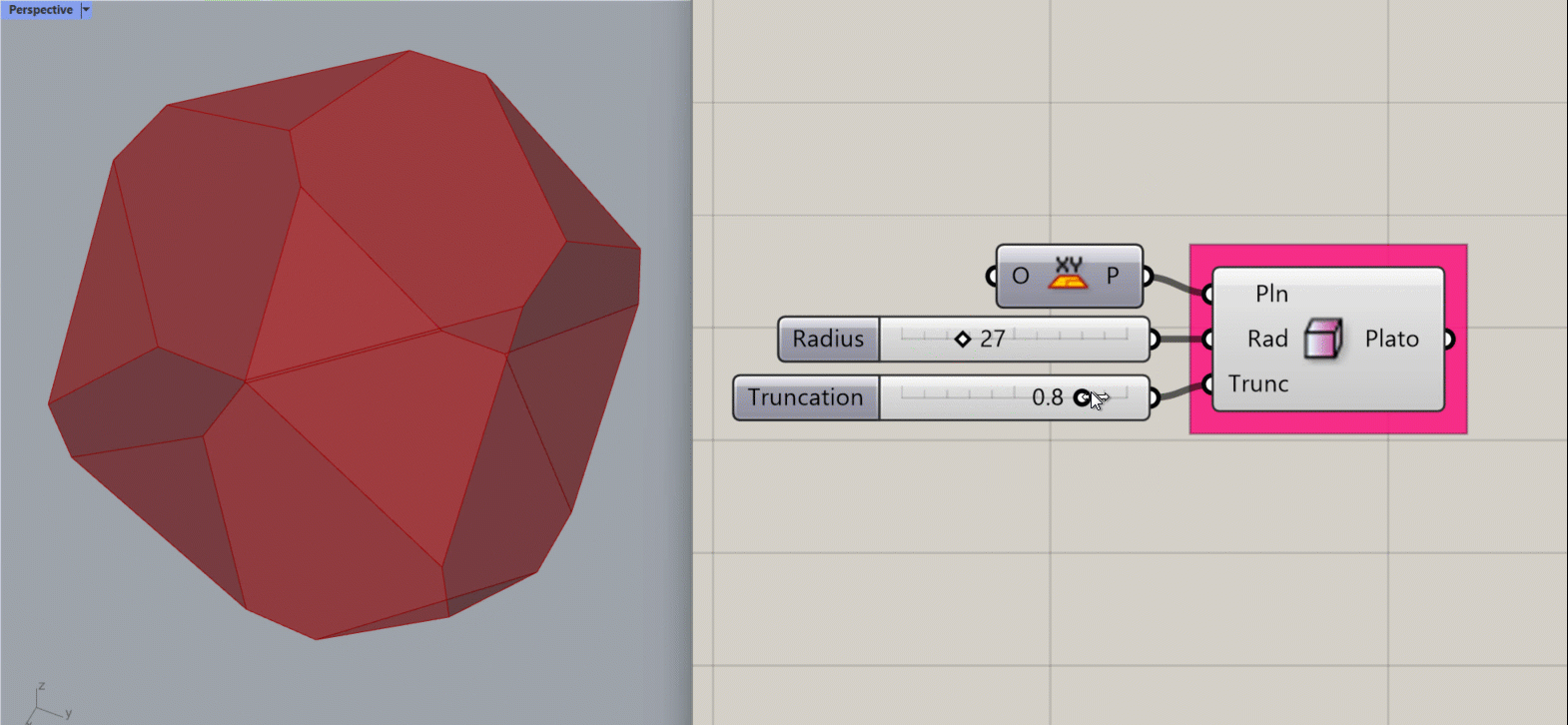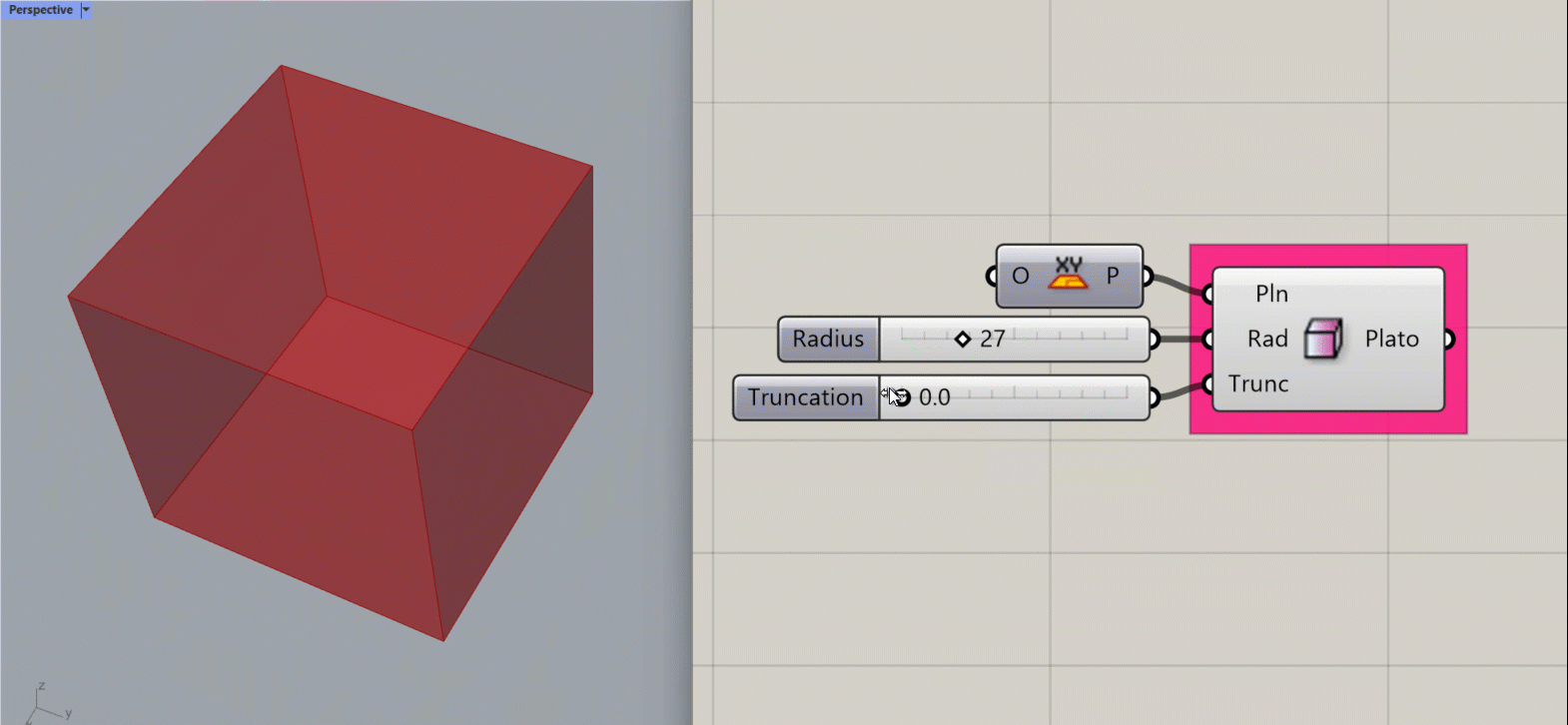
Platonic Cube
Creates a mathematical Platonic Cube about a specified plane.
Input:
- A list of planes, which will determine the location(s) of the results.
- An integer for the radius of a sphere. The resulting platonic form will fit inside the sphere.
- An integer between 0 and 1 to determine the amount of truncation at the corners of the cube. This adjusts also the object’s size to fit inside the radius of the theoretical sphere.
Results:
- A list of platonic cubes.
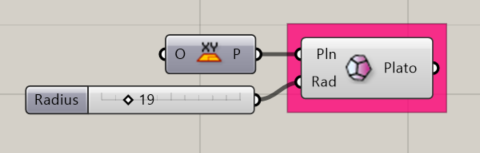
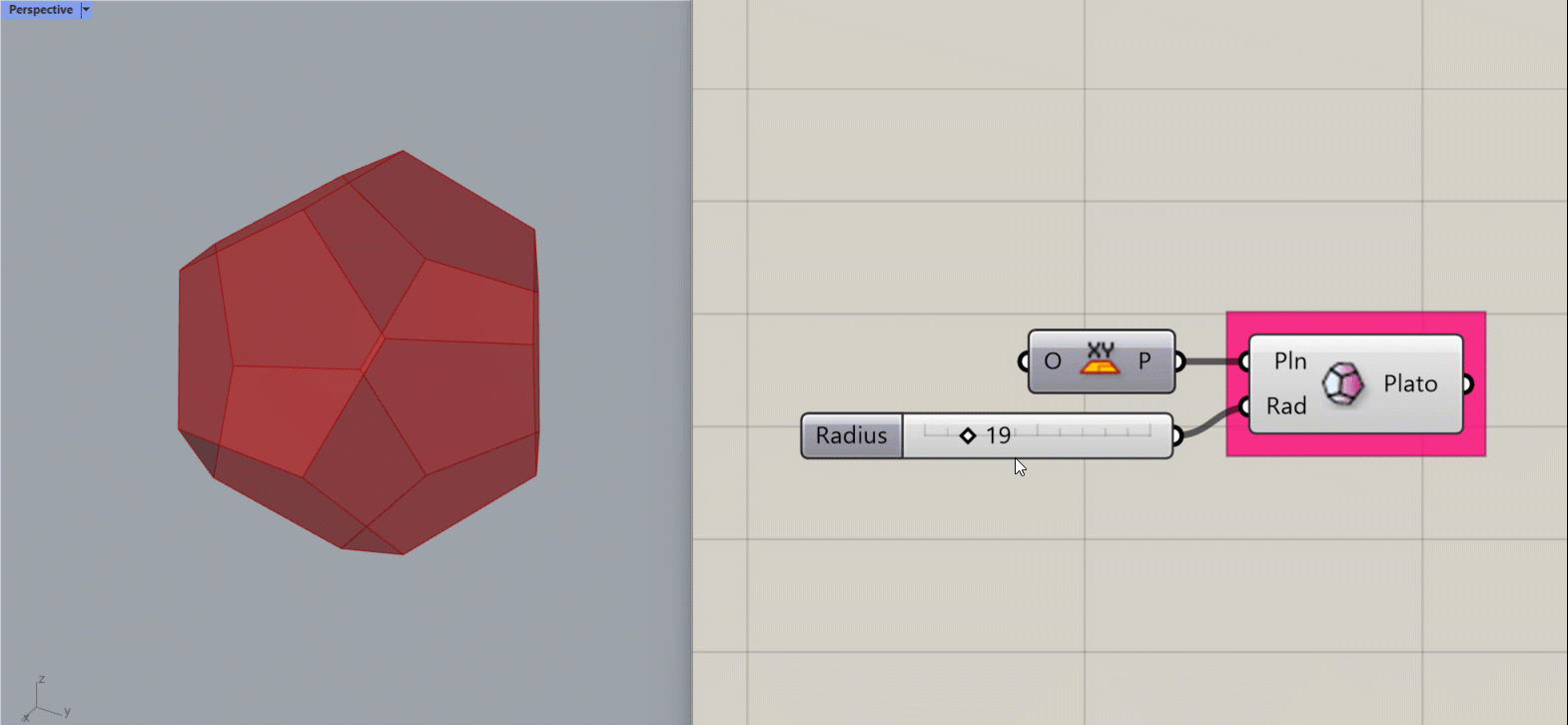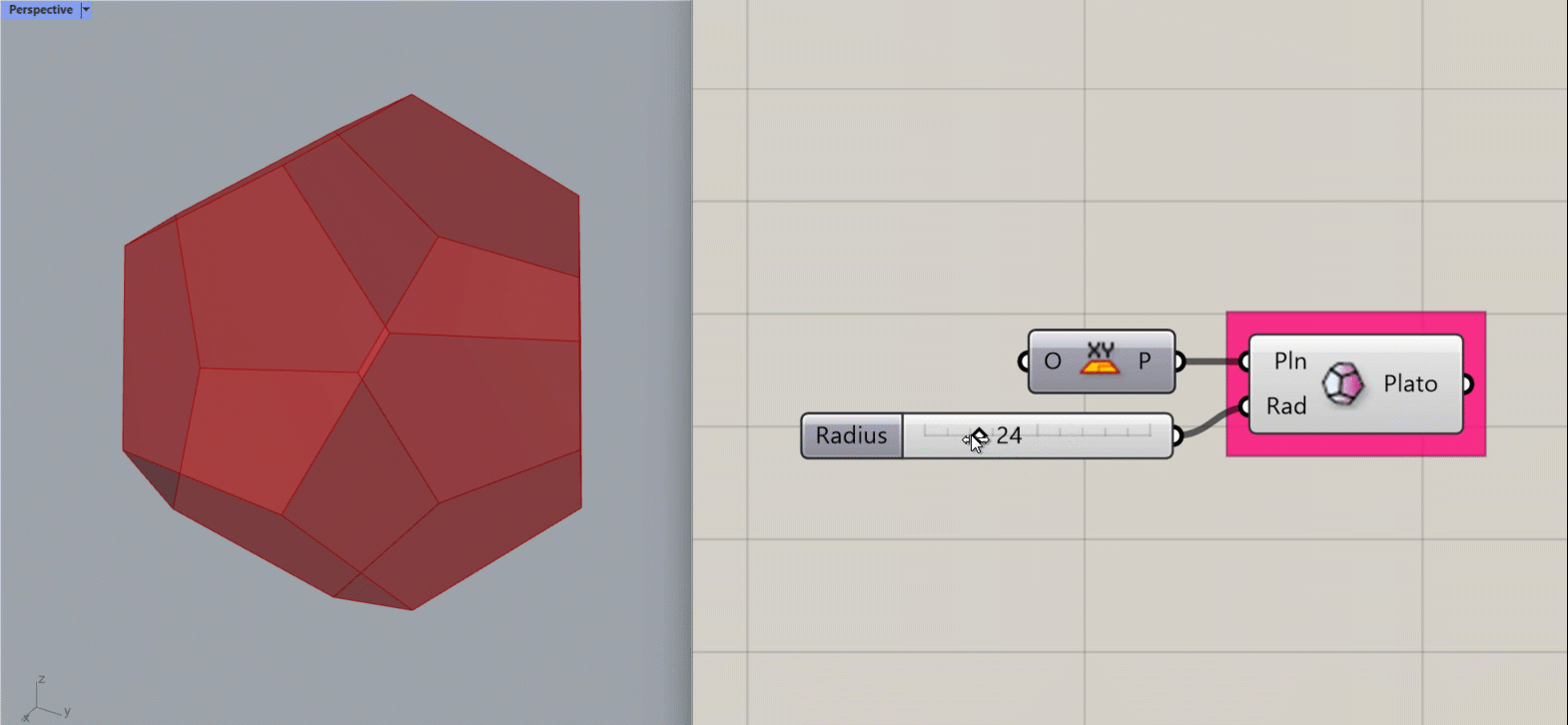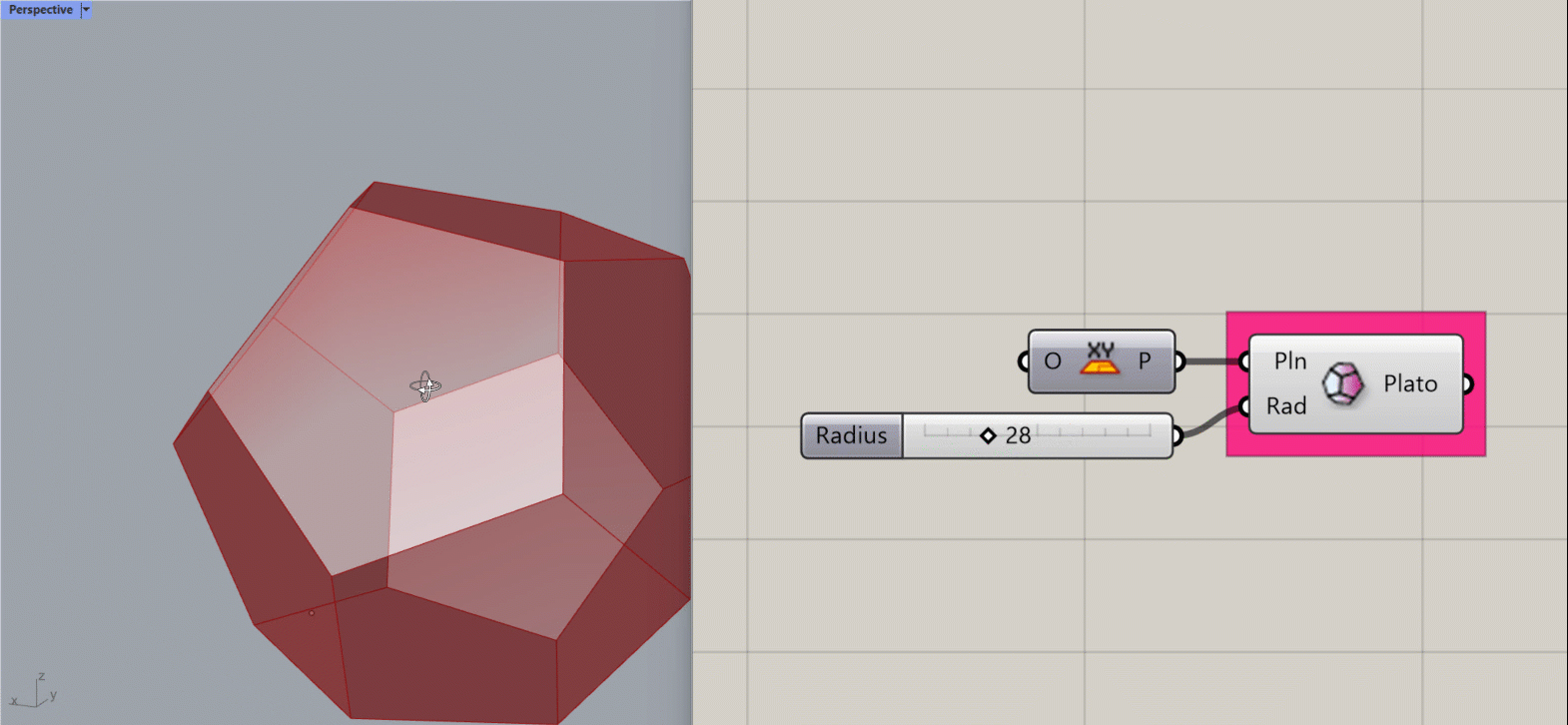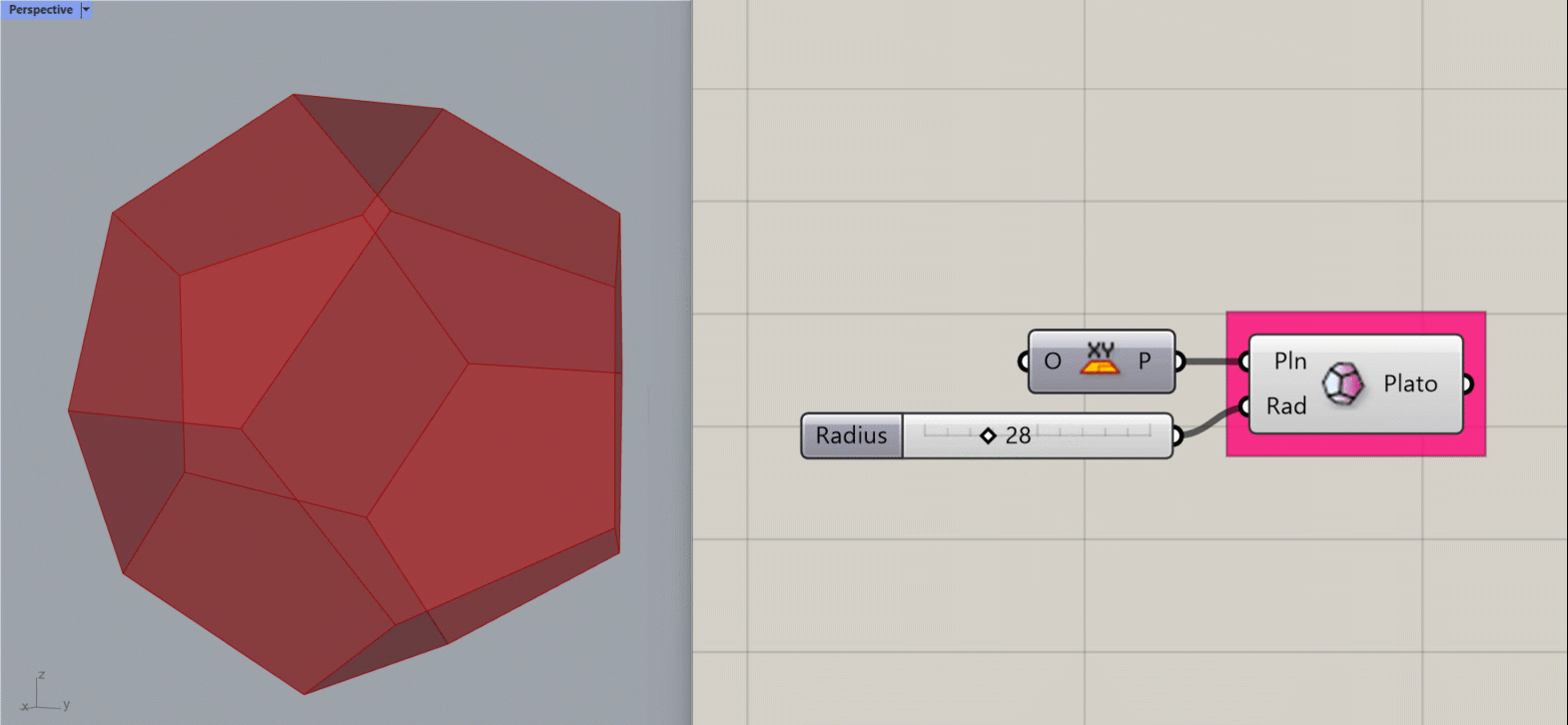
Platonic Dodecahedron
Creates a Platonic Dodecahedron about the given plane.
Input:
- A list of planes, which will determine the location(s) of the results.
- A integer to set the Radius of the object
Results:
- A platonic dodecahedron shape
Platonic Icosahedron
Creates a Platonic Icosahedron about the given plane.
Input:
- A list of planes, which will determine the location(s) of the results.
- An integer for the Radius of the shape.
- An integer between 0 and 1 to determine the amount of truncation at the corners of the shape.
Results:
- A Platonic Icosahedron
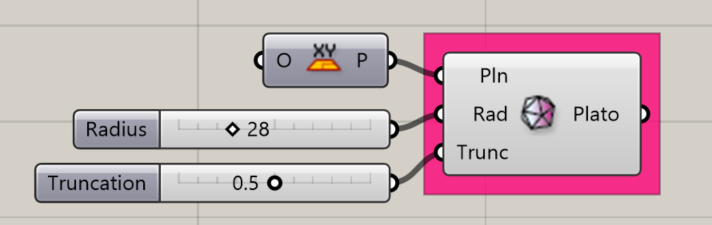
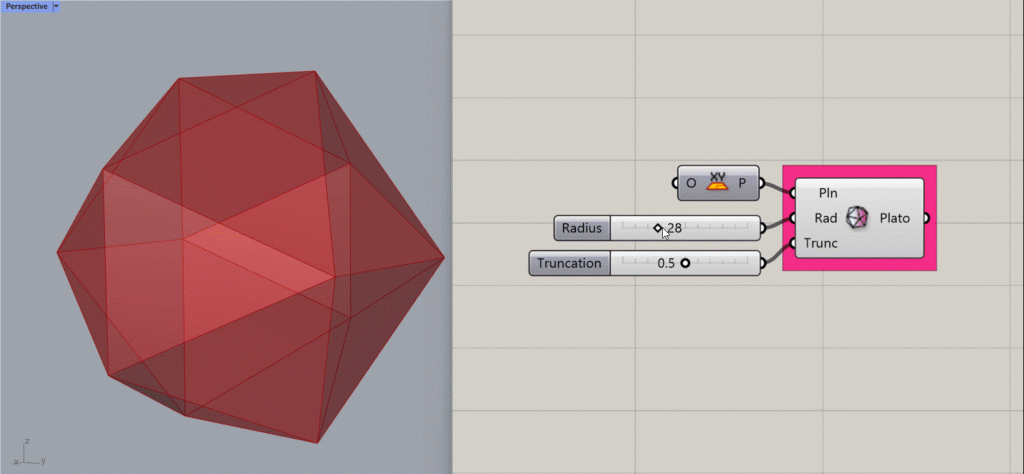
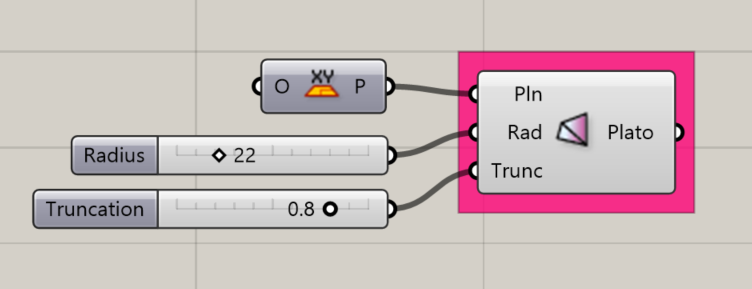
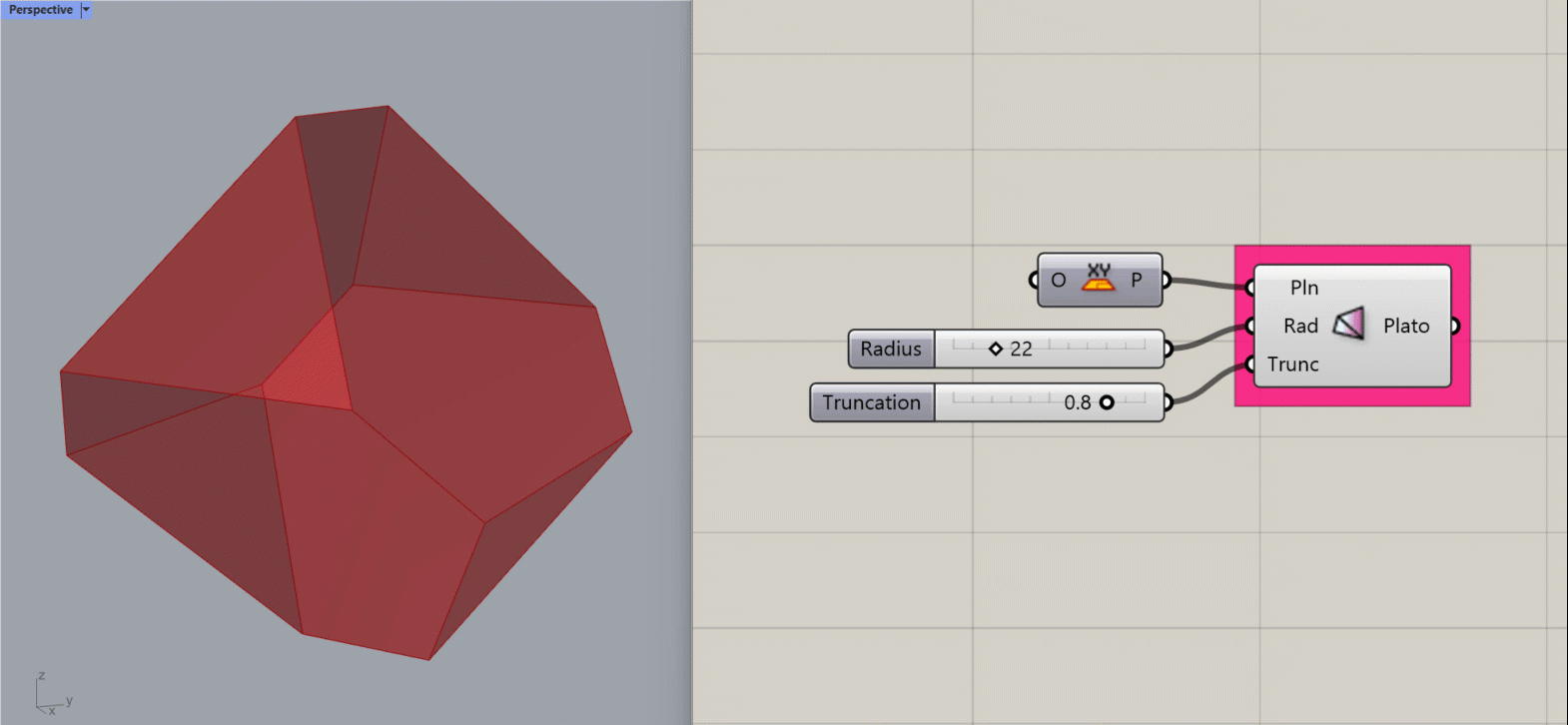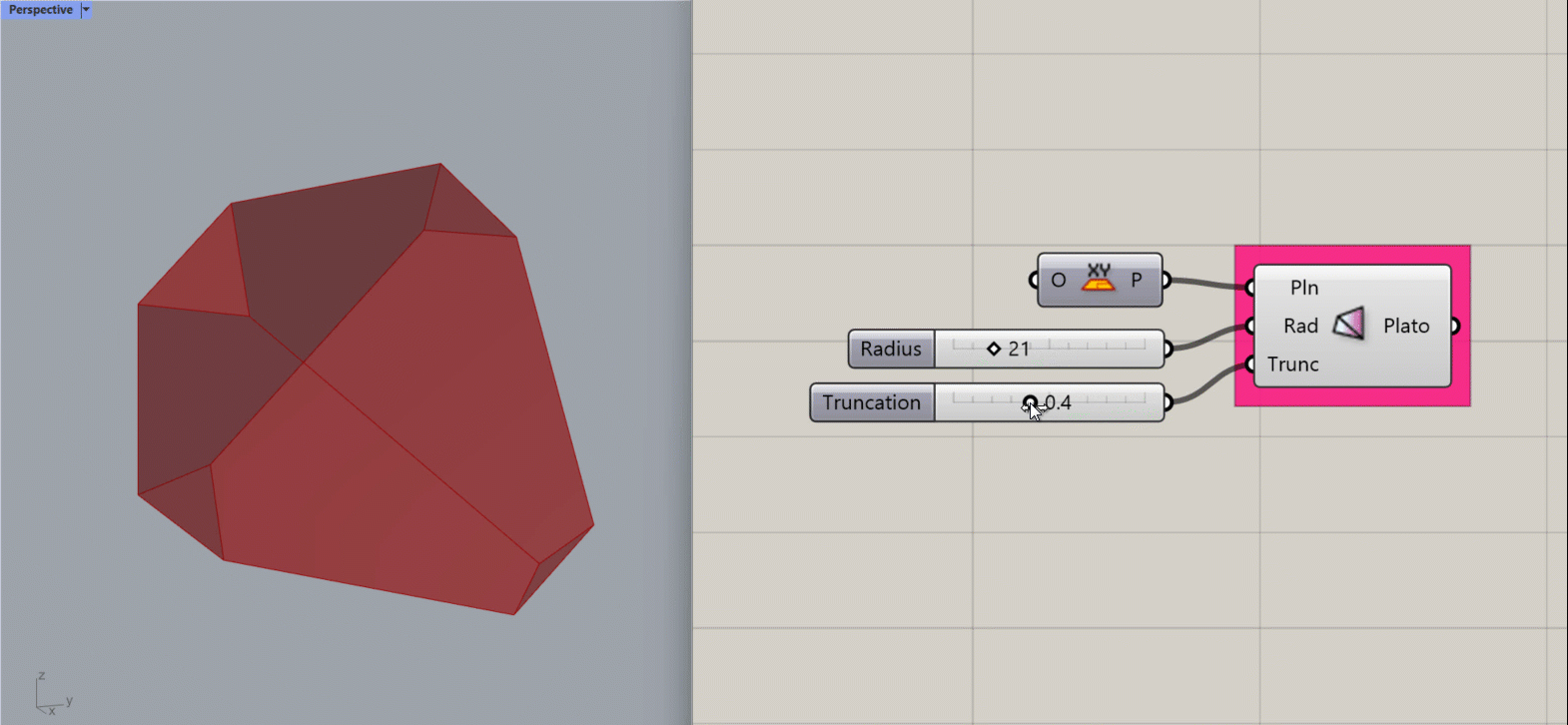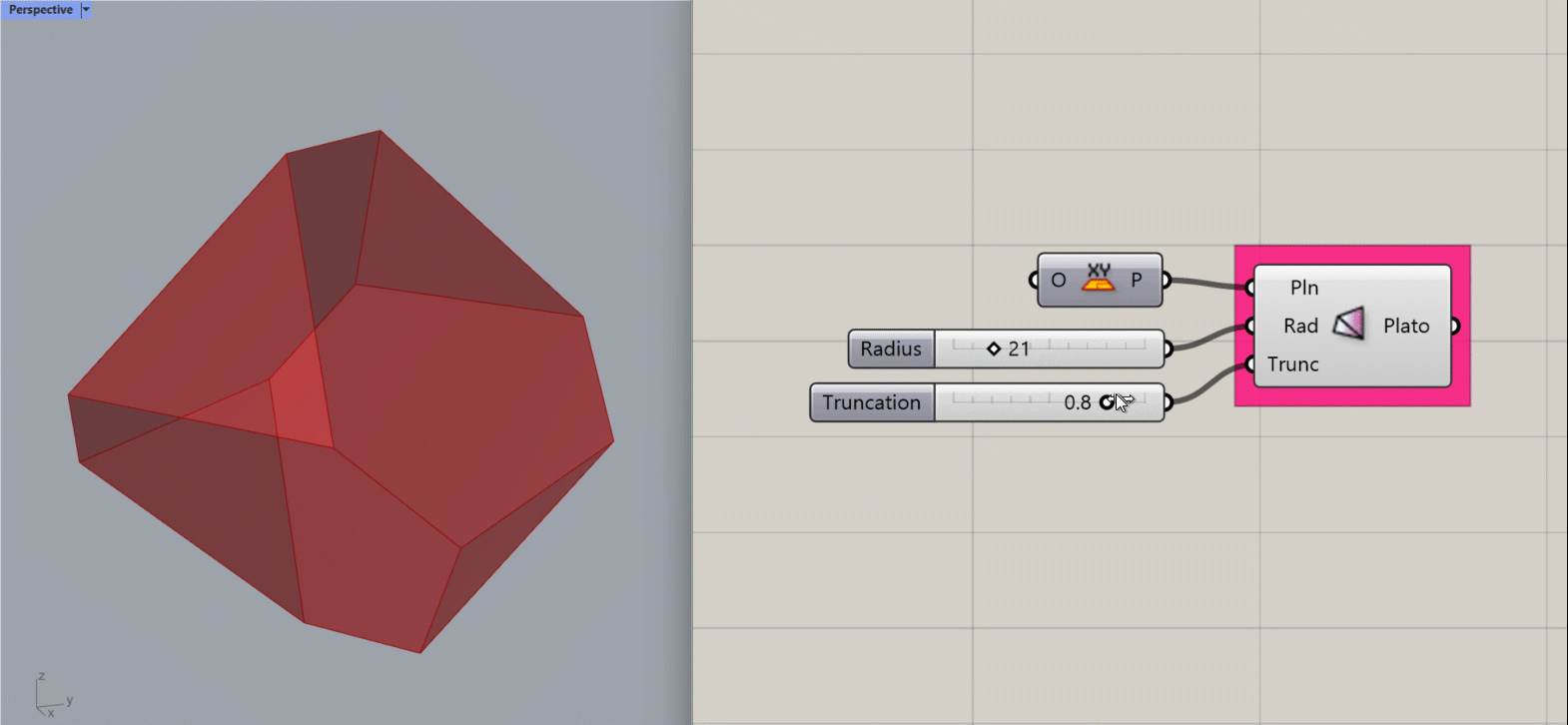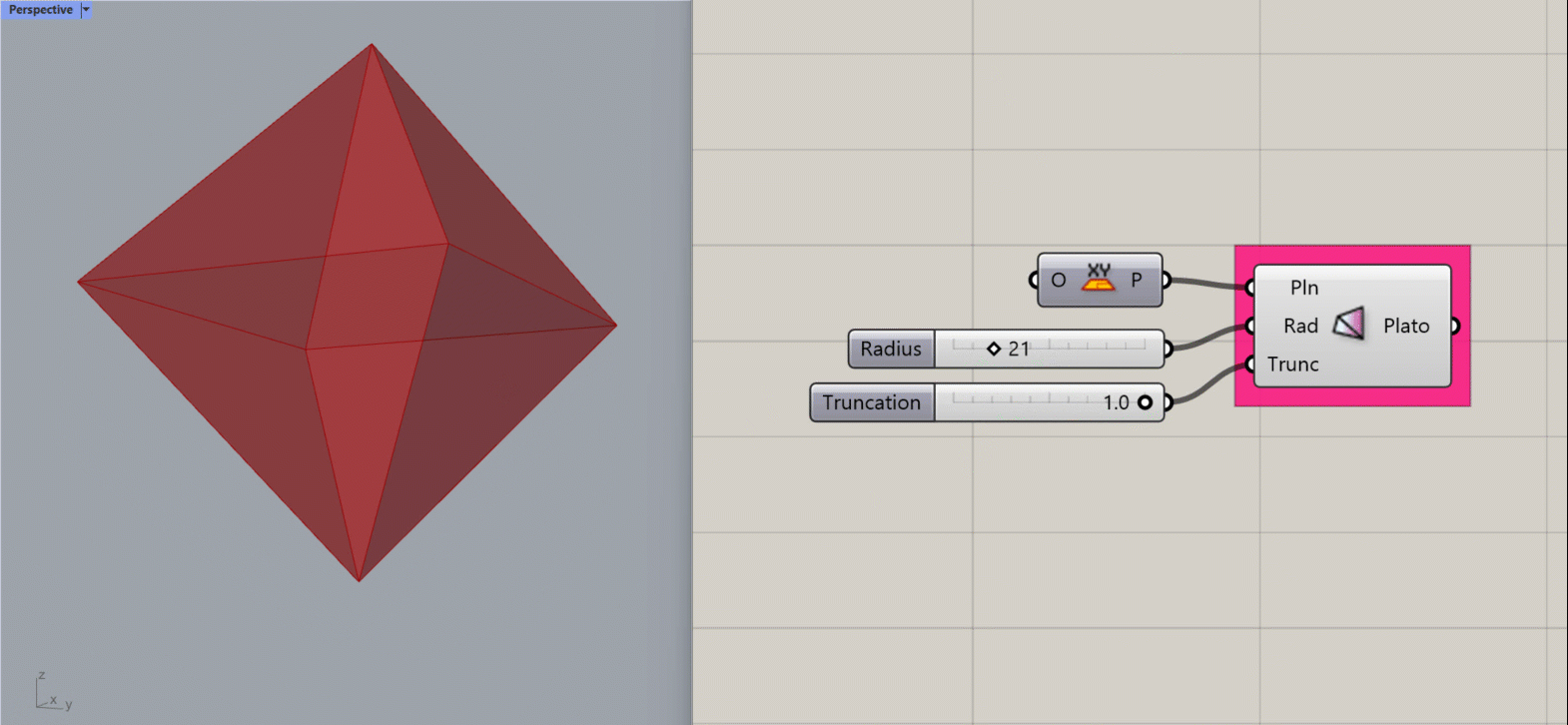
Platonic Octahedron
Creates a Platonic Octahedron about the given plane.
Input:
- A list of planes, which will determine the location(s) of the results.
- An integer for the Radius of the shape.
- An integer between 0 and 1 to determine the amount of truncation at the corners of the shape.
Results:
- A platonic octahedron
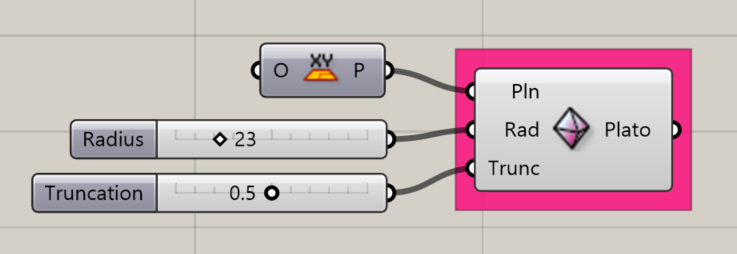
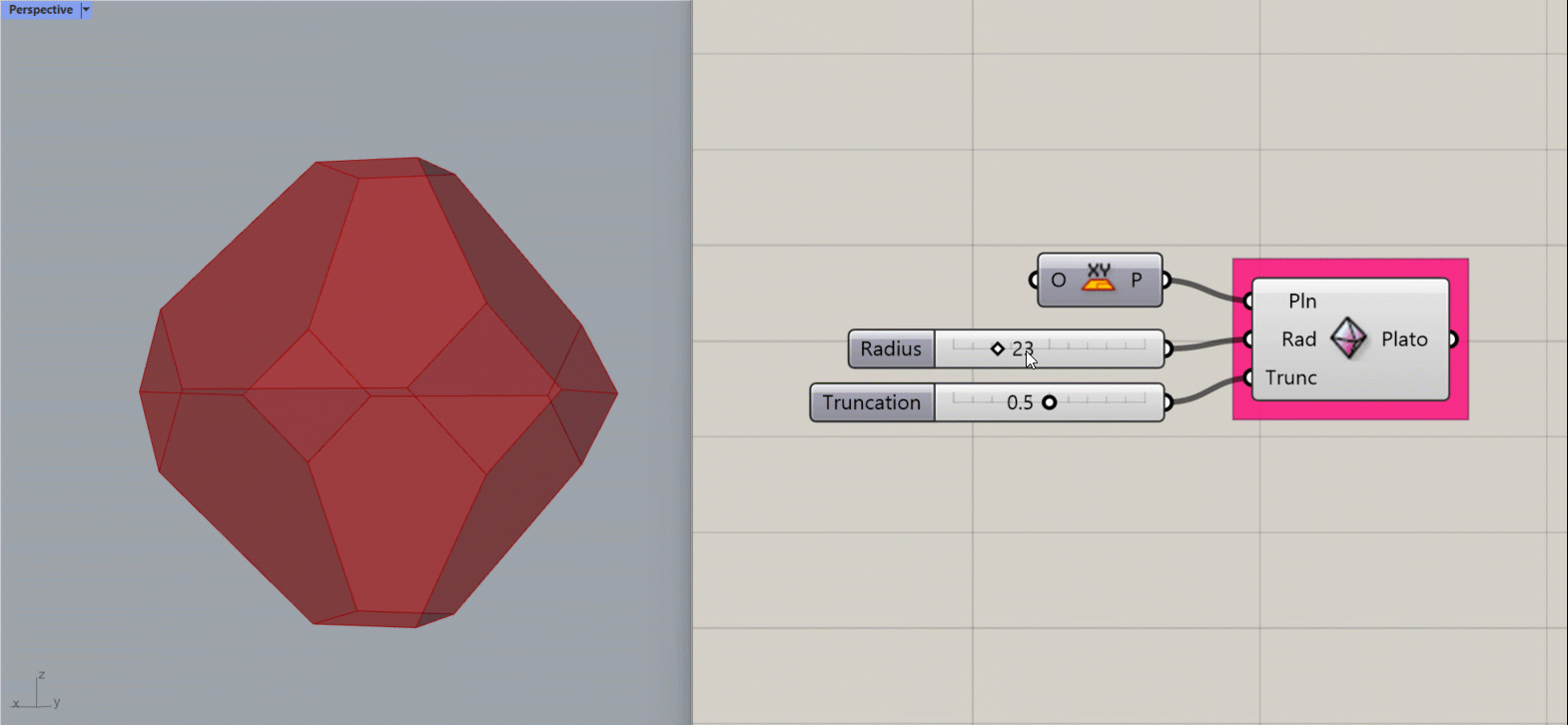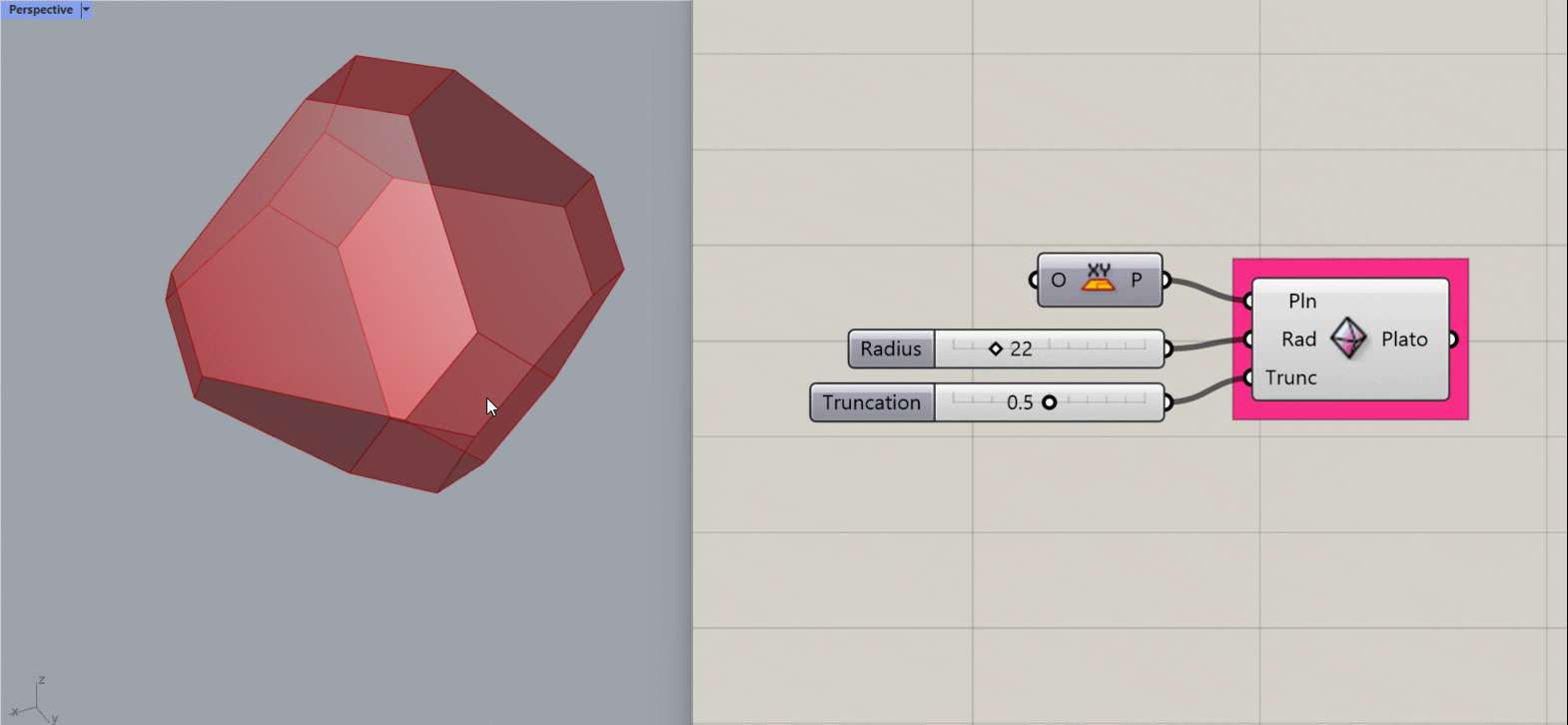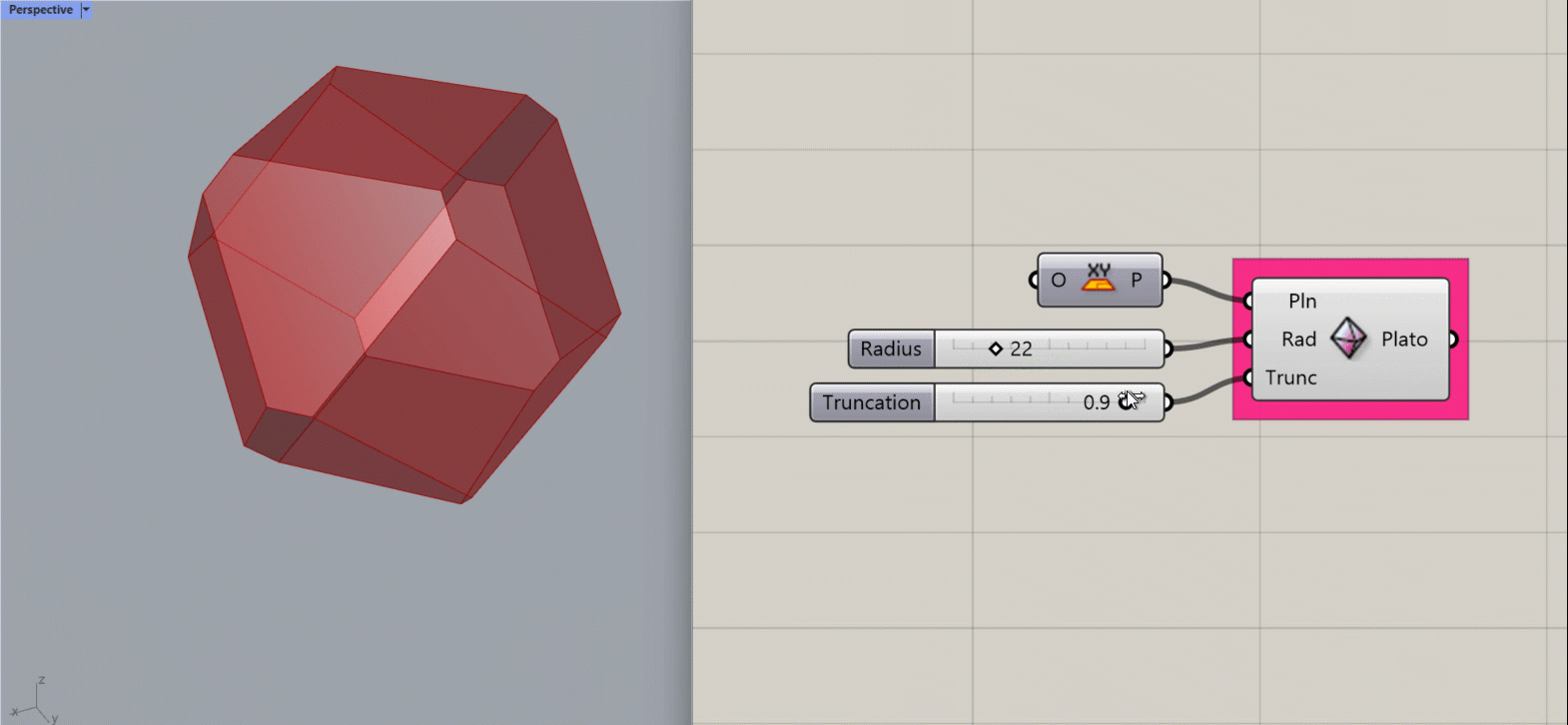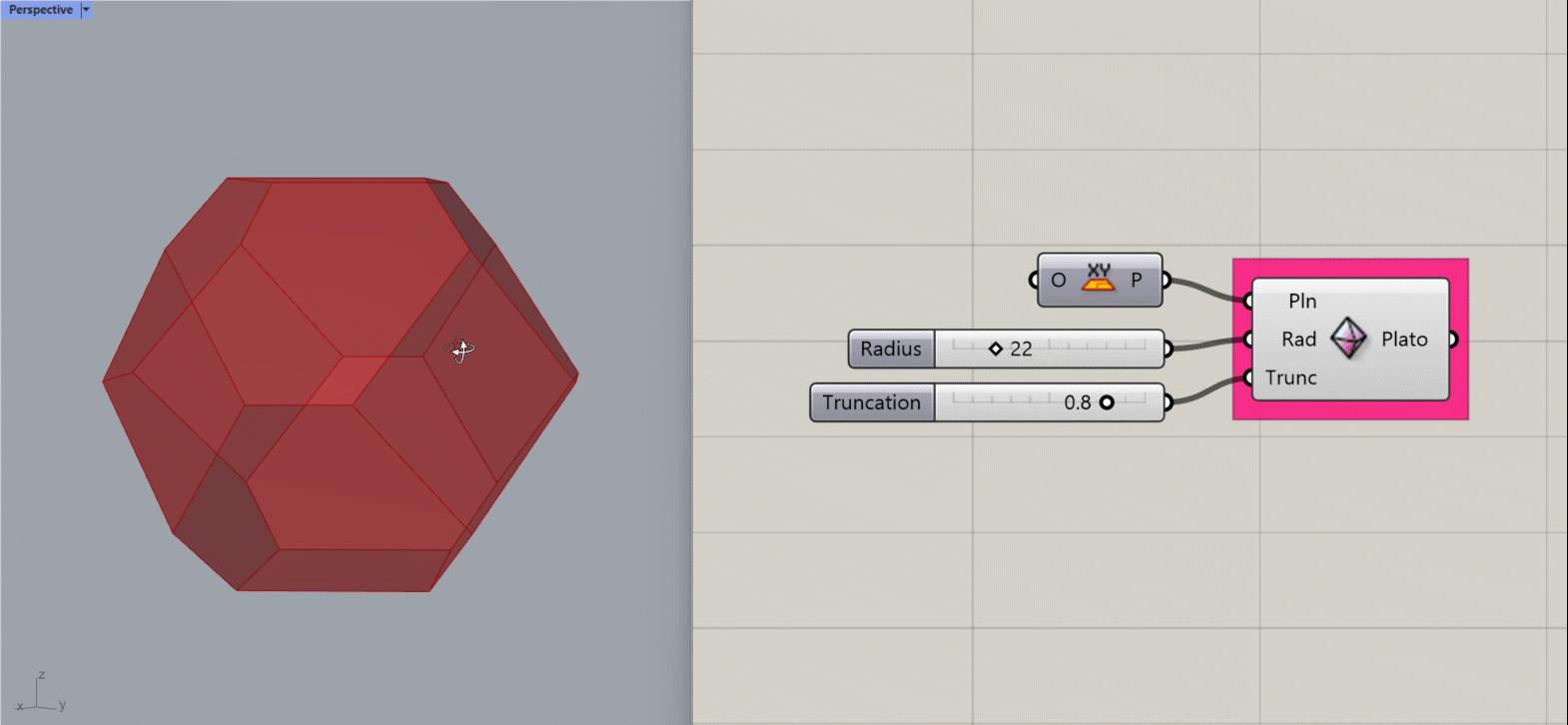
Platonic Tetrahedron
Creates a Platonic Tetrahedron about the given plane.
Input:
- A list of planes, which will determine the location(s) of the results.
- An integer for the Radius of the shape.
- An integer between 0 and 1 to determine the amount of truncation at the corners of the shape.
Results:
- A platonic tetrahedron